delenie_mnogochlena

Какво означава да разделим един полиномPна другQ? Това означава намиране на полиномиM(частно) иN(остатък), които отговарят на две изисквания:

1) има равенство:MQ + N = P;

2) степента на полиномаNе по-малка от степента на полиномаQ.

Полиномно делениеможе да се извърши по следния начин:

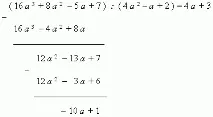
1) Разделете първия член 16a³ от дивидента на първия член 4a² от делителя; резултатът 4aе първият член на частното.

2) Умножаваме получения израз 4aпо делителя 4a²– a +2 ; запишете резултата 16a³–4a²+8aпод дивидента (един подобен член под другия).

3) Изваждаме термин по член този резултат от дивидента и премахваме следващия по ред член на дивидента 7; получаваме остатъка 12a²–13a +7 .

4) Разделете първия член 12a² от този израз на първия член 4a² от делителя; резултат 3 е вторият член на частното.

5) Умножаваме този втори член на частното 3 по делителя 4a²- a +2 и отново записваме резултата 12a²-3a +6 под дивидента (един подобен член под другия).

6) Извадете член по член резултата, получен от предишния остатък и получете втория остатък:–10a +1. Степента му е по-малка от степента на делителя, така че делението завършва.

В резултат на това получихме частното 4a +3 и остатъка–10a +1.

Деление на полином на линеен бином

Линеен бином. Теорема на Безу.

Линеен биноме полином от първа степен:a x + b.Ако разделим полинома, съдържащ букватаxна линейния биномx–b, къдетоbе някакво число (положително илие отрицателен), тогава остатъкът ще бъде само полиномот нуластепен (вижтепараграф "Делене на полиноми"), т.е. някакво числоN, което може да се определи без намиране на частното. По-точно, това число е равно на стойността на полинома, получен чрезx=b.Това свойство следва оттеоремата на Безу:полином a0xm+ a1xm-1+ a2xm- 2+ …+ amсе дели на бинома x – b с остатък N = a0bm+ a1bm-1+ a2bm-2+ …+ am.

---