ДИСКРИМИНАНТНАТА КРИВА е
обикновено диференциално уравнение от първи ред F(x, y, y')=0е набор от точки (x, y) на равнината, чиито координати удовлетворяват уравнението (x, y)= 0,, получено чрез изключване наy'от отношениятаF=0иF'y=Oили чрез изключване наx'от отношенията G=0 иGxr=0,където G(y, x, x')=F(x, y,x') (приемайки, чеF'yсъществува). :
1) е решение на уравнениетоF=0,във всяка точка
където уникалността е нарушена, в този случай D. c. е обвивката на семейството от интегрални криви (напримерy=1иy=-1 за уравнениетоy' 2 +y 2 -1 = 0, фиг. 1;
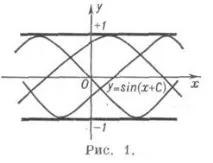
y=0за уравнението y' 3 -y 2 =0, фиг. 2);
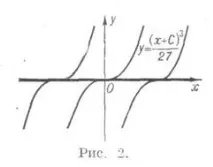
2) да бъде решение на уравнениетоF=0,във всяка точка от което има уникалност (напр. y = 0 за уравнението y' 2 -y 2 =0, фиг. 3);
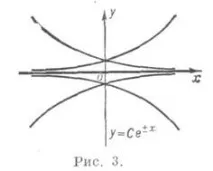
3) да не е решение на уравнениетоF=0,в този случай, D. до. има набор от ръбове на интегрални криви (например x=0 за уравнениетоy' 2 -x=0,Фиг. 4),
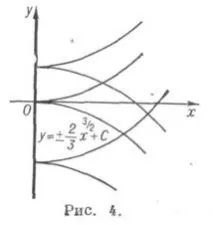
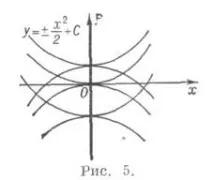
или допирни точки на различни интегрални криви (напримерx=0за уравнениетоy' 2-x 2 =0, фиг. 5).
Ние също така разглеждаме уравнениетоF=0в комплексната област, когато F е полином вy'(виж, например, [2], глава II).
Спр.: [1] J. Sansone, Обикновени диференциални уравнения, прев. от италиански, т. 2, М., 1954; [2] В. В. Голубев, Лекции по аналитична теория на диференциалните уравнения, 2 изд., Москва-Ленинград, 1950 г.
Математическа енциклопедия. - М .: Съветскиенциклопедия. И. М. Виноградов. 1977-1985 г.
Вижте какво е "ДИСКРИМИНАНТНАТА КРИВА" в други речници:
Специално решение на диференциално уравнение, решение, в което уникалността е нарушена във всяка точка (вижте Диференциални уравнения). За уравнението y = f(x, y) това означава, че през всяка точка от O. r. преминава през няколко различни интегрални криви ... Велика съветска енциклопедия