Двуизвадков тест за вариация F-тест в MS EXCEL
Обмислете използването на MS EXCEL при тестване на статистически хипотези за равенството на дисперсиите на 2 нормални разпределения. Нека изчислим стойността на тестовата статистика F0, разгледаме процедурата "F-тест с две проби", изчислим P-стойността (P-стойност), изградим доверителен интервал. Нека направим „F-тест с две проби за дисперсия“, като използваме добавката Analysis Package.
Има две независими случайни променливи с нормално разпределение. Тези случайни променливи имат нормални разпределения с неизвестни дисперсии σ1 2 и σ2 2, съответно. От тези разпределения бяха получени две проби с размер n1 и n2.
Необходимо е да се провери хипотезата за равенството на дисперсиите на тези разпределения (англ. Hypothesis Tests for the Equality of Variances of Two Normal Distributions).
СЪВЕТ: Тестването на хипотези изисква познаване на следните понятия:
Забележка: Тестване на хипотези за дисперсията на нормалното разпределение (тест с една извадка) е описано в статията Тестване на статистически хипотези в MS EXCEL за дисперсията на нормалното разпределение.
Нулевата хипотеза H0 звучи така: дисперсиите на нормалните разпределения са равни, т.е. σ1 2 = σ2 2 .
Алтернативна хипотеза H1: σ1 2 <> σ2 2 . Тези. трябва да тестваме двустранна хипотеза.
За разлика от z-теста и t-теста, където разглеждахме разликата между средните стойности, в този тест ще разглеждаме отношението на дисперсиите: σ1 2 / σ2 2 . Ако дисперсиите са равни, то съотношението им трябва да е равно на 1.
Както е известно, стойността на дисперсията на извадката s 2 може да служи като точкова оценка на дисперсията на разпределението σ 2 . Съответно, оценката на съотношението на дисперсиите σ2 2 / σ2 2 ще бъде s1 2 / s2 2 .
Процедурата за проверка на хипотезата за равенството на дисперсиите на 2разпределения има специално име: двуизвадков F-тест за дисперсии (F-тест: Тестове на хипотези за дисперсии на две нормални разпределения).
Тестовата статистика за проверка на хипотези от този тип е случайната променлива F= s1 2 / s2 2 .
Тази тестова статистика, както всяка друга случайна променлива, има свое собствено разпределение (в процедурата за тестване на хипотези това разпределение се нарича „референтно разпределение“, английски Reference distribution). В нашия случай F-статистиката има F-разпределение (разпределение на Фишер). Стойността, която е взела F-статистиката, се обозначава с F0.
Забележка: В статията Статистика и техните разпределения е показано, че извадковото разпределение на статистиката
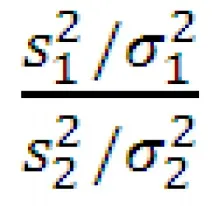
Нека зададем необходимото ниво на значимост α (алфа) (грешката от първия вид, разрешена за този проблем, т.е. вероятността за отхвърляне на нулевата хипотеза, когато е вярна).
Ние ще отхвърлим двустранната нулева хипотеза, ако F0, изчислено от извадките, е:
- по-голям от горния α/2-квантил на F-вероятностното разпределение с n1-1 и n2-1 степени на свобода, или
- по-малко от долния α/2-квантил на същото разпределение.
Записваме критерия за отклонение, като използваме горните квантили:
За да изчислите стойността на долния квантил на α/2-квантила в MS EXCEL, използвайте формулата =F.OBR(α/2; n1-1, n2-1) или =F.OBR.RT(1-α/2; n1-1, n2-1)
В примерния файл е предоставен двустранен тест за хипотеза.
F-тестът обикновено се използва за отговор на следните въпроси:
- Двете проби взети ли са от популации с еднакви дисперсии?
- Направете промените втехнологичен процес (нова термична обработка, подмяна на химически компонент и т.н.), за да се намали променливостта на текущия процес?
СЪВЕТ: Преди да тествате хипотези за равенство на дисперсиите, е полезно да начертаете двуизмерна хистограма, за да определите визуално разпространението на данните в двете проби.
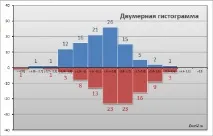
Доверителен интервал
В примерния файл за двустранен F-тест се изчисляват границите на съответния двустранен доверителен интервал.
Примерният файл също така показва еквивалентността на тестване на хипотеза в доверителния интервал, F0 статистика (F-тест) и p-стойност (вижте по-долу).
Изчисляване на P-стойност
При тестване на хипотези, в допълнение към F-теста, широко разпространен е друг еквивалентен подход, базиран на изчисляването на p-стойността (p-стойност).
Ако p-стойността е по-малка от даденото ниво на значимост α, тогава нулевата хипотеза се отхвърля и алтернативната хипотеза се приема. Обратно, ако p-стойността е по-голяма от α, тогава нулевата хипотеза не се отхвърля.
В случай на двустранна хипотеза p-стойността се изчислява, както следва:
Защо се изчислява двойната вероятност? Нека си представим, че нивото на достоверност е зададено на 0,05 и F0 Забележка: Можете също да прочетете за p-стойността в статията за z-теста с две проби.
Функция F.TEST()
Функцията F.TEST() връща p-стойност в случай на двустранна хипотеза.
Функцията има само 2 аргумента: array1 и array2, които съдържат препратки към диапазони от клетки, съдържащи селекции.
Така функцията F.TEST() е еквивалентна на горната формула =2*MIN(F.DIST(F0; n1-1; n2-1; TRUE); F.DIST.RT(F0; n1-1; n2-1))
където F0 е съотношението на дисперсиите на извадката, n1 и n2 са размерите на извадката.
Функцията F.TEST() може да се използва и когатотестване на едностранни хипотези - за това трябва да разделите резултата му на 2.
Пакет за анализ
Добавката F-Test Analysis Package има специален инструмент: F-Test Two Sample for Variances.
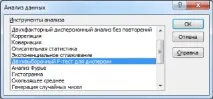
След като изберете инструмент, ще се отвори прозорец, в който трябва да попълните следните полета (вижте примерния файлов лист Analysis package ):
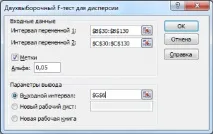
В резултат на изчисленията зададеният интервал на изхода ще бъде запълнен.
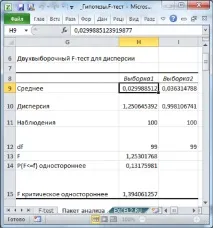
Същият резултат може да се получи с помощта на формули (вижте примерния файлов лист Analysis Package):
Нека анализираме резултатите от изчисленията, извършени от добавката:
- Средно: средно за двете проби. Изчисленията могат да бъдат направени с помощта на функцията AVERAGE(). Средните стойности не са включени в изчисленията за тестване на хипотези и са дадени само за информация;
- Дисперсия: дисперсии на двете проби. Изчисленията могат да бъдат направени с помощта на функцията VARP.B().
- Наблюдения: размер на извадката. Изчисленията могат да се извършват с помощта на функцията COUNT().
- Df: брой степени на свобода: n-1, където n е размерът на пробите;
- F: стойността на тестовата F-статистика (в нашата нотация това е F0, съотношението на дисперсиите на извадката);
- P(F2> σ2 2 . Еквивалентна формула =F.DIST.RT(F0;n1-1; n2-1) );
- F Критична една опашка: Горният α-квантил на F-разпределението с n1-1 и n2-1 степени на свобода. Еквивалентна формула =F.OBR.PH(α; n1-1; n2-1) .