Урок – Примерни задачи за конструиране

Кратко описание на документа:

Продължавайки да овладявате решението на строителни проблеми, е необходимо да проучите подробно основните методи за решаване на различни проблеми. Видео урокът "Примерни задачи за конструиране" е насочен към развиване на едно от най-важните умения в геометрията - провеждане на правилни построения и намиране на решения на геометрични задачи чрез конструиране.

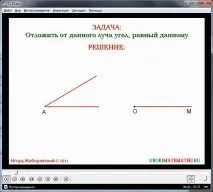
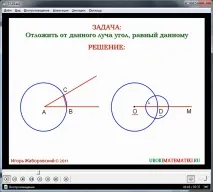
Първият пример за задача, решена с обикновена линийка и пергел, е построяването на ъгъл, който е равен на даден. Условието на задачата се показва на екрана. Решението започва с образа на лъча OM и ъгъла ∠A. Пояснява се, че условието на задачата означава, че е необходимо да се построи ъгъл, равен на построения ъгъл ∠A, така че една от страните на получения ъгъл да е лъчът OM. За да се реши тази задача, се предлага първо да се начертае окръжност с някакъв радиус с център в точка A. Маркират се пресечните точки B и C на тази окръжност с лъчите на ъгъл ∠A. След това се начертава същата окръжност с център в началото на лъча OM. Отбелязва се пресичането на окръжността с лъча в точка D. След това е необходимо да се измери с компас разстоянието между точките B и C, принадлежащи на ъгъла ∠A, и да се построи окръжност с измерения радиус, където центърът е в точка D. За по-нататъшно изграждане вниманието на ученика се насочва към точките на пресичане на тази построена окръжност с първата окръжност. Отбелязваме една от пресечните точки като точка E. По построение ъгъл ∠MOE е ъгълът, равен на ъгъл ∠A. Доказателство за този факт е дадено въз основа на съществуващите знания за признаците на равенство на триъгълниците. За да се докаже равенството на ъглите, е необходимо да се разгледат триъгълниците ΔABC и ΔОДE. Равенството на страните AB=OD и AC=OE следва от построението, тъй като те са радиуси на една и същакръгове. В този случай CB = ED чрез конструиране на малък кръг, тъй като неговият радиус е приет равен на CB. Използвайки третия критерий за равенство на триъгълниците, ние твърдим, че тези триъгълници са равни. И съответните ъгли на еднакви триъгълници са равни по двойки, така че равенството ∠A=∠MOE е вярно. С помощта на линийка и пергел се построява ъгъл, равен на даден. Отбелязва се също, че при решаване на практически задачи на земята по този начин би било възможно да се построи ъгъл, равен на дадения с въже.
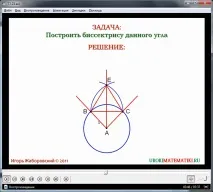
Вторият пример за задача е построяването на ъглополовяща. Условието на задачата се показва на екрана. При решаването, като начало, се показва ъгълът ∠BAC. От центъра на дадения ъгъл се изчертава окръжност с произволен радиус. Отбелязани са пресечните точки на тази окръжност с точките, принадлежащи на страните на ъгъл ∠BAC. След това трябва да нарисувате два кръга, чиито центрове са тези пресечни точки. В пресечната точка на построените окръжности се образуват две точки. Сред тези точки една се намира в ъгъла. Ние го обозначаваме като точка E. За да намерите тази точка, не е необходимо да изобразявате тези кръгове изцяло - достатъчно е да начертаете частите, в които се намира точката на тяхното пресичане, разположена вътре в ъгъла. Това е направено на показаната фигура. Проблема решен. А сега нека докажем, че резултатът от конструкцията - отсечката OE - е ъглополовяща на ъгъла. За да се докаже валидността на преценката, е необходимо да се разгледат триъгълниците ΔABE и ΔACE. Тези триъгълници са равни по три страни (по третия знак за равенство на триъгълниците). AB \u003d AC като радиуси на построената окръжност, страната AE е обща за два триъгълника, а BECE по конструкция като радиуси на еднакви начертани окръжности. Еднаквите триъгълници имат съответните страни, равни по двойки. Това означава, че ъглите ∠BAE=∠CAE също ще бъдат равни.Следователно лъчът AE дели дадения ъгъл на две равни части и е негова ъглополовяща. Примерът показва, че един ъгъл може да бъде разделен на две равни части с помощта на пергел и линейка. По същия начин можете да разделите ъгъла на четири равни части, като първо го разделите наполовина, а след това всеки от ъглите също наполовина. Материалът е допълнен с интересни факти, свързани с проблема за трисекция на ъгъл. Учениците са информирани, че е невъзможно да се раздели ъгъл на три части с линийка и пергел. Доказателството за това твърдение е направено през XIX век.
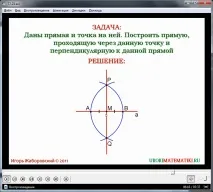
Третият пример е изграждането на перпендикулярни линии. Условието на задачата се показва на екрана. Като начало се начертава права линия с отбелязана точка върху нея. През дадена точка е необходимо да се начертае права, перпендикулярна на дадената. Под условието е изобразена права a с отбелязана точка M. С помощта на пергел отбелязваме равни отсечки на лъчите MA и MB. След това трябва да начертаете две окръжности с центрове в точки A и B. Маркирани са пресечните точки на тези окръжности P и Q. През тези точки се начертава права линия. Тази линия ще бъде желаната линия, перпендикулярна на a. Нека докажем, че това твърдение е вярно. За да направите това, разгледайте триъгълника ΔRAB. Този триъгълник е равнобедрен, тъй като неговите страни RA и RV са равни по конструкция - те са радиуси на еднакви окръжности. PM е медианата на посочения триъгълник. А в равнобедрените триъгълници медианата е и височина - съответно тя е перпендикулярна на АВ, следователно и на правата а.
Четвъртата задача е да се построи средата на отсечката. На екрана се извежда условието на задачата, след което се дава необходимата конструкция. На права линия е отбелязана отсечка AB, чиято среда трябва да се намери. С пергел отбелязваме радиуса с размера на дължината на отсечката AB иначертайте кръгове с даден радиус. Отбелязани са пресечните точки на окръжностите - P и Q. След начертаване на права линия, свързваща точките P и Q, се образува точка O на пресечната точка на отсечката PQ и правата. Тази точка е средата на сегмент AB.

Доказателството, че O е средата на AB се основава на равенството на триъгълниците ΔAPQ и ΔBPQ. Действително АР=РВ и АQ=QB като равни радиуси на окръжности по построение. PQ е общата страна на триъгълниците. От равенството на триъгълниците следва равенството на ъглите ∠ORA=∠ORV. В равнобедрен триъгълник ΔARB ъглополовящата RO също е медиана. Това означава, че отсечката AB е разделена от точка O на две равни части, тоест O е средата на отсечката.

Видео урокът "Примерни задачи за конструиране" може да се използва от учителя в урока като средство за онагледяване при разглеждане на решаване на задачи за конструиране. Също така този материал може да се използва при самостоятелно изучаване на материала и при дистанционно обучение.