Елипсоид на инерцията Уикипедия
Инерционният елипсоид (за точка O)е геометрична фигура под формата на повърхност от втори ред, която характеризира тензора на инерцията на твърдо тяло спрямо точка O.
Инерционният момент на тялото се определя по общата формула:
I = ∫ r ⊥ 2dm _^\,dm>
Тензорът на инерцията за твърдо тяло се представя като симетрична матрица
( I x x I x y I x z I y x I y y I y z I z x I z y I z z ) I_&I_&I_\\I_&I_&I_\\I_&I_&I_\end>>
в който елементите са инерционните моменти спрямо различни оси:
I x x = ∫ ( y 2 + z 2 ) d m =\int (y^+z^)\,dm> I y y = ∫ ( x 2 + z 2 ) d m =\int (x^+z^)\,dm> I z z = ∫ ( x 2 + y 2 ) d m =\int (x^+y^)\,dm>
I x y = I y x = − ∫ x y d m =I_=-\int xy\,dm> I x z = I z x = − ∫ x z d m =I_=-\int xz\,dm> I y z = I z y = − ∫ y z d m =I_=-\int yz\,dm>
Матрицата на инерционния тензор може да бъде представена в диагонална форма и тогава диагоналните елементи I x>gt; , Iy > , Iz > са главните инерционни моменти на тялото. След това уравнението за елипсоида на инерцията се записва като:
I x x 2 + I y y 2 + I z z 2 = 1 x^+I_y^+I_z^=1>
В този случай координатните оси на елипсоида трябва да съвпадат с главните оси на тялото.
Познаването на елипсоида на инерцията ви позволява да намерите инерционния момент на тялото около всяка ос, стига тя да минава през центъра на елипсоида. За да направите това, по избраната ос се начертава радиус-вектор, докато се пресече с елипсоида на инерцията. Инерционният момент на тялото около тази ос се определя от:
I=1r2 >>> , където r е дължината на радиус вектора.

Нека кутията има размери a, b, c. Основни моменти на инерция:
I x = m 12 ( b 2 + c 2 ), I y =m 12 ( a 2 + c 2 ), I z = m 12 ( a 2 + b 2 ) =>(b^+c^),\квад I_=>(a^+c^),\квад I_=>(a^+b^)>
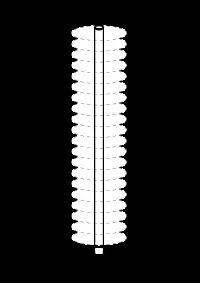
На илюстрацията е показан приблизителен изглед на елипсоида на инерцията.
За да се изчисли елипсоидът на инерцията на безкрайно дълъг тънък прът, едно от измеренията се счита за много по-голямо от останалите и елипсоидът се изражда в цилиндрична повърхност.