Елипсоидът има

Повърхности от 2-ри ред в пространството

Концепцията за повърхност от втори ред като геометрично място на точките. Неизродените повърхности от втори ред включват елипсоид, елиптичен параболоид, хиперболичен параболоид, еднослоен хиперболоид и двуслоен хиперболоид.

Общо повърхностно уравнение от втори ред

Ax2 + By2 + Cz2 + 2Fyz + 2Gzx + 2Hxy + 2Px + 2Qy + 2Rz + D = 0,

където x, y, z са координатите на точките на повърхността, A, B, C, . − реални числа.

Класификация на повърхности от 2-ри ред. Ранговете на матриците e и E, детерминантата на матрицата E и знаците на корените на характеристичното уравнение за матрицата e се използват като инварианти

# Ранг (e) Ранг (E) Δ Знаци k Външен вид на повърхността

1 3 4 0 Идентичен въображаем елипсоид

3 3 4 > 0 Разни Еднолистов хиперболоид

4 3 4 0 Разни Хиперболичен параболоид

9 2 3 Идентичен елиптичен цилиндър

10 2 3 Идентичен въображаем елиптичен цилиндър

11 2 3 Разни Хиперболичен цилиндър

12 2 2 Разни пресичащи се равнини

13 2 2 Еднакви въображаеми пресичащи се равнини

14 1 3 Параболичен цилиндър

15 1 2 Успоредни равнини

16 1 2 Въображаеми успоредни равнини

17 1 1 Съвпадащи равнини

Конична повърхност.

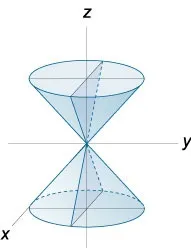
Въображаема конична повърхност

Конусът бива реален и въображаем Конус от втори ред е повърхност, чието уравнение в някаква декартова координатна система има вида Пресечната точка на конуса с равнината се нарича връх на конуса.

въображаем_

Елипсоидът е реален и въображаем. Повърхността, определена в някаква правоъгълна декартова координатна система от уравнението a > 0, b > 0, s > 0, нареченоелипсоид Елипсоидът е ограничена повърхност, тъй като неговото уравнение предполага това

Елипсоидът има

централна симетрия относно началото,

аксиална симетрия спрямо координатните оси,

---