Foundation_geometrii_OZO - Страница 4

Ако линиите се пресичат, тогава оста на симетрия е

ъглополовящата на всяка двойка вертикални ъгли е

риболовни линии, образувани от тези линии

Нека a и b не се пресичат.

Нека А b, АР a (фиг.). Нека M AP , MN b .

Нека s = AP, x = AM.

Нека f ( x ) е дължината на перпендикуляра MN е непрекъсната функция. Нека ( x ) = s - x е непрекъснато

Тъй като f (0) f ( s )>gt; ( s ), тогава x 0 (0; s ): f ( x 0 ) = ( x 0 )

Нека M 0 е точка от отсечката AR, съответстваща на x 0 . Тъй като (x 0) = PM 0,

тогава (M 0, a) = (M 0, b).

M 0 N 0 b . RM 0 N 0 е равнобедрен. Нека начертаем от - ъглополовящата на ъгъла PM 0 N 0 - оста на симетрия на правите a и b. 

Теорема 5. Ако правата b е успоредна на правата a в дадена посока, тогава правата a е успоредна на правата b в същата посока.

Правите a и b са успоредни по предположение.

Нека B b . По лема 1 има ос на симетрия

Нека A е точка, симетрична на B спрямо c

( A a ). Нека докажем, че всеки лъч d с начало A,

минаваща вътре в ъгъла BAa пресича b.

Нека d' е лъч, симетричен на d по отношение на

прав c. Тъй като b a , след това b c и a c , тогава лъчът d'

пресича правата a в някакво t.M. Тогава лъчът d

пресича правата b в точката M', симетрична на M

спрямо правата с . 

Теорема 6 . Ако правите a и b са успоредни на c в дадена посока, тогава те са успоредни една на друга в същата посока.

5.2.3. Различни линии

Определение . Две прави се наричат разминаващи се, ако не се пресичат и не са успоредни.

През всяка точка извън дадена права минават две успоредни на нея прави и безкрайно много прави, отклоняващи се отнея. Всички те лежат в една от двойките ъгли, образувани от успоредни прави.

Теорема 7. Две линии, перпендикулярни на трета линия, се разминават Доказателство (UIRS)

Нека a c , b c . Те не се пресичат (от теоремите на абсолютната геометрия)

От друга страна, ако a b, тогава ъгълът на успоредност, който прави правата a

с перпендикуляр c , ще бъде равно на / 2 , което противоречи на теорема 2, раздел 6.2.1. 

Теорема 8 . Две линии, които при пресичане с трета образуват равни или съответни ъгли, разположени на кръст, се разминават.

Нека a и b се пресичат с

O - средата на сегмента AB. ИЛИ a, OQ b.

Тъй като OBQ = OAP (по конвенция), тогава OBQ = OAP

(от равенството на n/y триъгълници).

Тогава OP и OQ лежат на една и съща права линия, към която a

и b са перпендикулярни => a и b се разминават

Теорема 9 . Всякакви две разминаващи се прави имат един общ перпендикуляр, от двете страни на който се отдалечават една от друга за неопределено време.

Теорема 10 . Две успоредни прави се приближават асимптотично една към друга в посока на успоредност и се отдалечават една от друга за неопределено време в обратна посока

5.2.4. Успореден ъгъл

Нека правите a и b са успоредни в някаква посока и нека A е произволна точка на права b.

Ъгълът на успоредност зависи от избора на точка А на

Няма две точки на правата b, в които

ъглите на успоредност са равни (в противен случай сумата от ъглите

образуваният четириъгълник би бил равен на

2, което е невъзможно).

Теорема 1. Ъгълът на успоредност в точка А по отношение на права а зависи само от разстоянието от точка А до права а

Нека са дадени прави a и a' и точки A и A':

Нека А b, A' b': a b , a' b' (засигурност, нали)

0 и 0 ' – ъгли на успоредност в точки A и A' по отношение на прави a и a' Да кажем 0 0 ' , за определеност 0 > 0'.

Нека отделим вдясно от лъча АР ъгъл, равен на ъгъла 0'. Тъй като по предположение: 0 ' 0 , тогава страната на този ъгъл, различна от AP , пресича правата a в някаква точка Q . На правата a' от точката P' по посока на успоредните прави a' и b' полагаме отсечката

P'Q' = PQ. Тогава APQ = A'P'Q' =>

PAQ = P'A'Q' , но тогава от лъча A'P' са положени два равни ъгъла в една посока, което е невъзможно 

Означаваме (A, a) = s. Тъй като големината на ъгъла на успоредност в точка А спрямо a се определя само от стойността s, тогава тя е функция на s: П( s )

В геометрията на Лобачевски тази функция играе важна роля. Нарича се функция

Свойства на функцията на Лобачевски

1. П( s ) е определено на интервала (0; + )

2. Стойностите на P( s ) са в интервала (0; / 2 )

3. (Теорема 2) Функцията на Лобачевски е монотонно намаляваща функция Доказателство

Нека AP е перпендикуляр на a от точката A a .

Нека А' АР , АР = s , A'P' = s' .

Нека докажем, че ако s' > s , след това П( s' ) s ).

Нека А b a , A' b' a в една посока, тогава b b' .

Нека е ъгъл, съседен на 0

Ако 0 ' + = , тогава линиите b' и b – се разминават, особено след като тази сума не може да бъде повече от =>

Теорема 3. Функцията на Лобачевски взема всички стойности от интервала (0; / 2).

Последица. Функцията П( s ) е непрекъсната на интервала (0; + ), когато s 0 П( s ) / 2 и

Непрекъснатостта на функцията П( s ) следва от факта, че тя е монотонна и приема всички стойности от интервала (0; / 2 ), граничните отношения следват от непрекъснатостта на функцията П( s ).

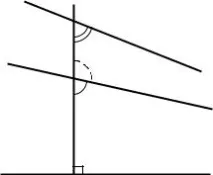
Забележка . В равнината на Лобачевски е възможно да се подредят три прави линии, което няма аналогия в равнината на Евклид.

Нека правите a и b са успоредни наляво. Те имат ос на симетрия s. На правата s вземете произволна точка A и начертайте лъч d, успореден на правата b вдясно. Вдясно от точка A на правата s има такава точка B, че перпендикулярът BC, прекаран в нея, е успореден на лъча d. Правата BC е успоредна на правата b. Тъй като правите a и b са симетрични на правата s, то правите BC и a също са успоредни. Така правите a и b са успоредни в една посока, правите b и BC са успоредни в друга, а правите a и BC са успоредни в трета.

Фигурата, образувана от правите a, b и BC, се нарича изроден триъгълник

или триъгълник с върхове в безкрайност.

5.3. Еквидистанция и хороцикъл

В геометрията на Евклид е известен факт - GMT, равноотдалечена от дадена права a и лежаща от едната страна на тази права, е права.

В клауза 1.4. беше показано, че това твърдение е еквивалентно на постулата V, следователно на равнината на Лобачевски това твърдение не е вярно. Нека дефинираме съответния GMT на равнината на Лобачевски и разгледаме неговите свойства.

Нека a е някаква права линия.

Дефинирайте . Съвкупността от точки, разположени от едната страна на правата a и на дадено разстояние от нея, се нарича еквидистант (хиперцикъл).

Правата a е основата на еквидистанта, перпендикулярът, пуснат от точката на еквидистанта към основата (и неговата дължина) се нарича височина на еквидистанта.

Теорема 1. Никакви три равноотдалечени точки не лежат на една и съща права Доказателство Нека точките A, B, C от еднакво отдалечената права лежат на една права.

Нека AA 1, BB 1, CC 1 са перпендикулярни на a.

Четириъгълник A 1 ACC 1 - четириъгълник Sak-

keri, който има 4 прави ъгъла, което е невъзможно на

и самолети на Лобачевски 

Последица. Всяка права линия, лежаща в равнината на равноотдалечената линия, пресича равноотдалечената линия в не повече от две точки.

Теорема 2. Всички точки на еквидистанта лежат от едната страна на правата t, прекарана през която и да е точка A на еквидистанта перпендикуляр на нейната височина AA' (от същата страна като основата a). Тази права е допирателна към еквидистантната права.

t X

A X 1

1. Тъй като t AA' и a AA' , то t и a се разминават. По този начин всички точки на линията t, различни от A, се отстраняват от линията a на разстояние, по-голямо от

2. Нека X е произволна точка от правата t, X' е проекцията на тази точка върху a, X 1 е пресечната точка на XX' с равноотдалечената права.

Ако X 1 A, то XX 1 0, а секансът AX 1 има гранично положение - права линия t. Така t е допирателна 

Теорема 3. За да бъдат равни две равноотстоящи прави е необходимо и достатъчно те да имат равни височини.

Еквидистантата има някои общи свойства с права линия и окръжност. И така, правата може да бъде "преместена по самата себе си", т.е. ако правата бъде преместена така, че нейните две точки A и B да съвпаднат с точките A' и B' на същата права, тогава правата във втората позиция ще съвпадне с оригиналната права. По същия начин с кръг, който може да се върти около центъра му и той ще се "плъзга сам".

Криви, които имат това свойство, се наричат криви на постоянна кривина. В геометрията на Евклид само прави линии и окръжности са такива криви. В геометрията на Лобачевски това свойство притежава и равноотдалечената линия. Ако основата A 1 на перпендикуляра AA 1 заедно с този перпендикуляр се премести по права линия a, тогава до-

край А на перпендикуляра ще опише еквидистанта, с такова движениееквидистантът ще се плъзне сам, т.е. има постоянна кривина. Еквидистантите с различни височини не могат да бъдат комбинирани от нито една от техните части, точно както кръгове с различни радиуси.

Други равноотдалечени имоти:

Една равноотдалечена линия е свързана със сноп от разминаващи се линии - множеството от всички линии, перпендикулярни на основата на равноотдалечената линия. Правите линии на този пакет се наричат равноотдалечени оси.

1. Равноотдалеченият е симетричен спрямо всяка своя ос. Доказателство

Нека u е основата на равноотдалечената линия и е една от нейните оси.

Нека M е произволна точка на равно разстояние , M 1

симетричен на точка M спрямо правата a, до

Нека M' и M' 1 са проекциите на точките M и M 1 върху правата

и тогава M' и M' 1 са симетрични по отношение на правата линия

моето a, така че MM' = M 1 M' 1 . Оттук следва,

2°. Във всяка равноотдалечена точка има допирателна, която е перпендикулярна на оста през допирателната точка.

Еднакво отдалечена хорда е всяка отсечка, която свързва две точки от една равноотдалечена права.

3°. Всяка права линия, съдържаща еднакво отдалечена хорда, е секанс с еднакъв наклон спрямо осите, минаващи през краищата на хордата.

Доказателство Нека AB е хордата на дадената равноотдалечена права, а AA' и BB' са нейните оси, където A' и B' са проекциите

точки A и B към основата на еквидистанта. По дефиниция на еднакви отсечки AA' и BB' са равни, така че ABB'A' е четириъгълник на Сакери: A'AB = B'BA. 

4°. Перпендикулярната ъглополовяща към всяка хорда на равноотдалечена права е нейната ос.

Теорема 4 . Каквито и да са успоредните прави a и b, през която и да е точка A от правата a минава единственият секанс с равен наклон спрямо тези прави.

Нека начертаем оста на симетрия l към правите a и b. Начертайте права през A m l

m b = B и (AB, a) = (AB, b)

Ако преместите t.B по правата b, тогава един от ъглите между лъча AB и правата b се увеличава, а този, който лежи по

същата страна на правата AB, ъгълът между лъча AB и

права линия намалява. 

Помислете за молив от линии, успоредни в една

дъска. Нека a е някаква линия на този молив, A

А . На всяка права линия m от молива, различна от a, има

има единствена точка M, така че AM е секанс

равен наклон на правите a и m. Много такива точки

M (включително A) се нарича хороцикъл. Директно дадено

лъч се наричат неговите оси.

Хороцикълът се определя от молив от успоредни прави и точка А на една от тях. Нека B е точка от хороцикъла, разгледайте хороцикъла ', определен от същия сноп и точка B. Така дефинираните хороцикли съвпадат.

Теорема 5. Никакви три точки от хороцикъл не лежат на една права Доказателство

Да приемем, че точките A, B, C на хороцикъла лежат на една и съща права, тогава ъглополовящите на отсечките AB и BC са успоредни и имат общ перпендикуляр, което е невъзможно 

Свойствата на хороцикъла са подобни на тези на окръжността и еднакво отдалечената права, но има още едно свойство, което окръжността и еднакво отдалечената права нямат.

Теорема 6 . Всички хороцикли са еднакви Доказателство

Нека хороциклите и ' са определени съответно от точките A и A' и осите a и a', минаващи през тях. Тогава, според аксиомата за мобилността, има движение, което съчетава точките A и A' и положителните посоки на осите a и a', следователно хороциклите и' 

5.4. Някои факти за геометрията на Лобачевски

1 . Всеки ъгъл съдържа в себе си такива точки, през които е невъзможно да се начертаят линии, пресичащи двете страни на ъгъла.

Тези. ако права, минаваща през такава точка, пресича едната странаъгъл, няма да пресича другата страна.

Наистина твърдението, че през всяка точка вътре в ъгъл винаги е възможно да се начертае линия, пресичаща двете страни на ъгъла, е еквивалент на V постулата (Legendre)

2. Какъвто и да е острия ъгъл, винаги има перпендикуляр към едната страна на този ъгъл, който не пресича другата страна.

3 . Какъвто и да е острия ъгъл, винаги има перпендикуляр към едната му страна, успореден на другата страна.

4 . В геометрията на Лобачевски има триъгълници, около които е невъзможно да се опише кръг.

Твърдението, че окръжност може да бъде описана около всеки триъгълник, е еквивалентно на V постулата на Евклид (Фаркаш Болай, вижте раздел 1.4.)

Перпендикулярът към хордата на равноотдалечената линия, прекаран през нейната среда и представляващ GMT, равноотдалечен от върховете на хордата, е права линия, перпендикулярна на основата на тази равноотдалечена права.

5. В близост до който и да е триъгълник, вписан в еднакво отдалечената права, е невъзможно да се опише окръжност.

Нека ABC е вписано в равноотдалечената права. AA' , BB' a (еквидистантна основа) AA'B'B – четириъгълник на Сакери,