фракталГерасимов - нов вид фрактали

Открих този фрактал, когато гледах интерференция на вълни на повърхността на река. Вълната се движи към брега, отразява се и се наслагва върху себе си. Има ли ред в моделите, които вълните създават? Нека се опитаме да го намерим. Помислете не за цялата вълна, а само за вектора на нейното движение. Нека направим "бреговете" гладки, за да улесним експеримента.
Експериментът може да се проведе върху обикновен лист хартия в кутия от ученически бележник.
Вземете правоъгълник със страни q и p. Изпратете лъч (вектор) от ъгъл до ъгъл. Лъчът се придвижва към една от страните на правоъгълника, отразява се и продължава да се движи към следващата страна. Това продължава, докато лъчът удари един от останалите ъгли. Ако размерът на страната q и p са взаимно прости числа, тогава се получава модел (както ще видим по-нататък - фрактал).
На снимката ясно виждаме как работи този алгоритъм.
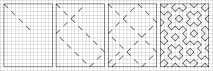

Най-удивителното е, че с различни страни на правоъгълника - получаваме различни модели.



Защо наричам тези модели фрактали? Както знаете, "фракталът" е геометрична фигура, която има свойствата на самоподобие. Част от картината повтаря цялата картина като цяло. Ако значително увеличим размерите на страните Q и P, става ясно, че тези модели имат свойства на самоподобие.
Нека се опитаме да увеличим. Ще се увеличим по хитър начин. Вземете, например, шаблон 17x29. Следните модели ще бъдат: 29x(17+29=46), 46x(29+46=75) . Една страна: (n); Втора страна: (n+1)=(n)+(n-1); 17, 29, 46, 75, 121, 196, 317, 513, 830, 1343 Като числата на Фибоначи, само с различни първи и втори членове на редицата: F(0)=17, F(1)=29.






Следващите фрактали се повтарят циклично.
Акопо-голямата страна е равномерна, получава се този модел:
Ако по-малката страна е четна:
Ако и двете страни са странни, получаваме симетричен модел:


В зависимост от това как започва лъчът: или
Ще се опитам да обясня какво се случва в тези правоъгълници.
Нека разделим квадрата от правоъгълника и да видим какво се случва на границата.
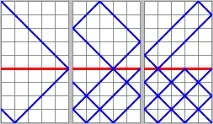
Лъчът излиза от същата точка, от която е влязъл.
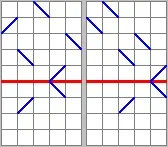
В този случай броят на квадратите, през които лъчът преминава, винаги е четно число.
Следователно, ако квадратът бъде отрязан от правоъгълника, немодифицираната част от фрактала ще остане.
Ако отделите квадратите от фрактала възможно най-много пъти, можете да стигнете до "началото" на фрактала.
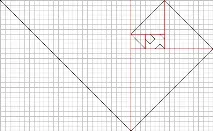
Прилича ли на спирала на Фибоначи?
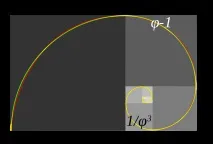
Фракталите могат да се получат и от числата на Фибоначи.
В математиката числата на Фибоначи (серия на Фибоначи, редица на Фибоначи) са числата: По дефиниция първите две цифри в редицата на Фибоначи са 0 и 1 и всяко следващо число е равно на сумата от предходните две. F(n)=F(n-1)+F(n-2) F(0)=0, F(1)=1
Както виждаме, колкото по-близо е пропорцията до златното сечение, толкова по-детайлен е фракталът.

В този случай фракталът повтаря част от фрактала, увеличена с .
Вместо числата на Фибоначи можете да използвате ирационални размери на страните:
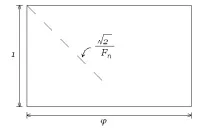
Получаваме същия фрактал.
Същите фрактали могат да се получат в квадрат, ако лъчът се изстреля от различен ъгъл:
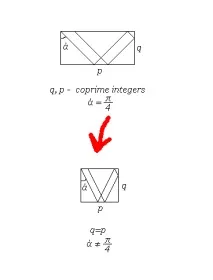
Какво може да се каже в заключение? Хаосът също е ред. С техните правила. Този ред не се изучава, но достаподлежащ на изучаване. И целият стремеж на науката е да открие тези закономерности. И накрая свържете частите от пъзела, за да видите голямата картина. Нека погледнем повърхността на реката. Ако хвърлите камък по него, вълните ще тръгнат. Кръгове доста податливи на изучаване. Скорост, период, дължина на вълната - всичко това може да се изчисли. Но докато вълната не достигне брега, тя няма да се отрази и няма да започне да се припокрива със себе си. Получаваме хаос (вмешателство), който вече е труден за изучаване Ами ако тръгнем от обратното? Опростете поведението на вълната колкото е възможно повече. Опростете, намерете модел и след това се опитайте да опишете пълната картина на случващото се. Какво може да бъде опростено? Очевидно, за да направите отразяващата повърхност права, без завои. Освен това, вместо самата вълна, използвайте само вектора на движение на вълната. По принцип това е достатъчно за изграждане на прост алгоритъм и симулиране на процеса на компютър. И дори напълно достатъчно, за да направим "модел" на поведението на вълната върху обикновен лист хартия в кутия. Какво имаме в резултат? В резултат на това виждаме, че при вълновите процеси (една и съща вълничка по повърхността на реката) имаме не хаос, а наслагване на фрактали (самоподобни структури) един върху друг.
Нека разгледаме друг вид вълни. Както знаете, електромагнитната вълна се състои от три вектора - вълнов вектор и вектор на електрически и магнитни полета. Както можете да видите, ако "хванем" такава вълна в затворена област - където тези вектори се пресичат, получаваме доста ясни затворени структури. Може би елементарните частици са същите фрактали?

Всички фрактали в правоъгълници от 1 до 80:

Затворени зони във фрактали:

Просто красив фрактал:
