Геометрични структури от данни, основни операции - Програмиране от
K lacc Point съдържа елементи с данни x и y за съхраняване на координатите на точката. Компонентните функции осигуряват операции за определяне на позицията на точка спрямо даден сегмент от права линия и изчисляване на разстоянието от дадена точка до права линия. Функциите на допълнителния компонент третират текущата точка като вектор и претоварват подходящите оператори, за да реализират векторна аритметика, като използват ключовата дума operator. Включени са и компонентни функции, които връщат стойности на полярен ъгъл и дължина.
К конструкторът инициализира нова точка с координати x и y:
Ако аргументът не е посочен, тогава точката в началото (O, O) се инициализира по подразбиране.
Можете да инициализирате точка като дубликат на друга точка. Например извикването Point p(q) инициализира нова точка p със същите координати като точка q. В този случай инициализацията се извършва от конструктора за копиране по подразбиране (съществуващ в C++ компилатора), който извършва копиране с всички елементи.
Векторно добавяне и векторно изваждане се извършват с помощта на функционални операции със знаци за операция + и - съответно:
Операцията за умножение с точка е реализирана като приятелска функция на класа Point, а не член на класа, тъй като нейният първи операнд не е от тип Point. Операторът се дефинира, както следва:
O operator-function [] връща x-координатата на текущата точка, ако стойността 0 е посочена като координатен индекс в извикването, или y-координатата, ако е посочена стойност на индекса 1:
Относно операцията за връзка == и != се използват за определяне на еквивалентността на две точки:
O операциите прилагат лексикографския ред на отношенията, когато се счита, че точка a е по-малка отточка b, ако или a.x Y подреждането на точки в равнината може да се направи по безкраен брой начини. Все пак е удобно да се използват оператори P. Преди да преминете към останалите компонентни функции на класа Point, разгледайте следния прост пример, който показва използването на обекти от класа Point.
Функцията за ориентация връща 1, ако трите обработвани точки са положително ориентирани, -1, ако са отрицателно ориентирани, или 0, ако са колинеарни.
Относителна позиция на точка и права линия
Една от най-важните операции е да се определи позицията на точка спрямо насочен сегмент от права линия. Резултатът от операцията показва дали точката лежи отляво или отдясно на насочената отсечка на правата или, ако съвпада с правата, се намира след края на насочената отсечка от тази права, преди началото, а ако не е нито едно от двете, то дали не съвпада с началото или края или се намира между тях. Насочен сегмент от права линия ясно разделя равнината на седем непресичащи се области и тази операция показва към коя от тези области принадлежи точката.
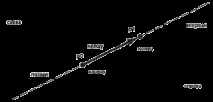 |
За да се определи позицията на текущата точка спрямо правата отсечка p0p1, насочена от точка p0 към точка p1, се използва функцията за класифициране на компонента. Връща стойност от тип enum, указваща позицията на текущата точка:
Първо се проверява ориентацията на p0, p1 и p2, за да се определи дали p2 е отляво или отдясно, или е колинеарно с p0p1. В последния случай са необходими допълнителни изчисления, ако векторите a=pl-pO и b=p2-p0 имат противоположна посока, тогава точката p2 лежи зад насочения сегмент p0p1ако векторът a е по-къс от вектора b, тогава точката p2 се намира след отсечката p0p1. В противен случай точката p2 се сравнява с точките p0 и p1, за да се определи дали съвпада с една от тези крайни точки или се намира между тях.
За удобство е предоставена малко по-различна версия на функцията за класифициране на компонента, която приема като аргумент ребро вместо двойка точки.
Определението на относителната позиция на точка и права линия се използва много често. В някои приложения е достатъчна по- груба класификация (т.е. достатъчно е да се посочи позицията на точка отляво или отдясно на права линия или просто да се фиксира съвпадение с нея). В други приложения е необходима пълна схема на тази класификация.
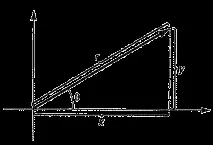
Полярната координатна система предоставя втори начин за определяне на позицията на точка в равнина. Полярната ос започва от началната точка 0 и е насочена под формата на хоризонтален лъч надясно, както е показано на фиг. 2. Точка a е представена от двойка числа (ra, Thetaa). Приемайки точката a като вектор, започващ от началото, числото ra определя вида на вектора, а Thetaa - неговия полярен ъгъл (ъгълът, образуван между вектора a и полярната ос и броен в посоката на въртене обратно на часовниковата стрелка).
Съответствието между двойки числа (ra, Thetaa) и точки не е едно към едно: много двойки могат да представляват една и съща точка. Двойката (0, Theta) съответства на началото за всяка стойност от 0. Освен това, двойките числа (r, Theta + 360k) съответстват на една и съща точка за всяко цяло число k.
Една точка може да бъде представена както в декартова, така и в полярна система
координати и понякога е необходимо да се премине от една система към друга. Както е очевидно от фиг. 2, два израза
извършват трансформации от полярникоординати (r, Theta) до декартови координати (x, y).
 |
За обратното преобразуване координатата на разстоянието се определя като
За да изразите полярния ъгъл Theta като функция от x и y, имайте предвид, че има връзка tan Theta = y/x, която предполага
За да използвате този израз във функцията polarAngle, е необходимо да правите разлика между квадрантите в равнината и да вземете предвид случая на възможна нулева координата x:
Имайте предвид, че функцията polarAngle връща -1,0, ако текущият вектор е нулев вектор (в противен случай връща неотрицателна стойност). Ще използваме това обстоятелство по-късно, за да опростим описанието на функцията за сравнение въз основа на спецификацията на полярния ъгъл.
Функцията за компонент на дължината връща дължината на текущия вектор
Функцията за компонент на разстоянието връща (подписаната) стойност на разстоянието от текущата точка до ръба. Тази функция ще бъде дефинирана по-долу.