Гравитационно привличане на сферични тела хомогенна сфера
Физика > Гравитационно привличане на сферични тела: хомогенна сфера
Научететеоремата на Нютон за обвивката с прости термини във физиката: гравитацията на сферично симетричен обект, концепцията за центъра на масата, добавянето на вектори в сила.
Според теоремата за черупката, сферично симетричен обект влияе върху други обекти, тъй като цялата му маса е концентрирана в централната част.
Учебна задача
- Изложете теоремата за обвивката за сферично симетрични тела.
Ключови точки
- Силата е векторна величина, така че векторното сумиране на всички части на обвивката допринася за общата сила, която е еквивалентна на едно измерване на сила, взето от центъра на сферата.
- Гравитацията върху обект в куха сферична обвивка е равна на нула.
- Гравитацията в хомогенна сферична маса е линейно пропорционална на разстоянието от центъра на масата на сферата.
- Центърът на масата е единствената точка в центъра на разпределението на масата в пространството, където векторите са приравнени към нула.
Универсална гравитация за сферично симетрични тела
Гравитационната сила между две точки на маса е пропорционална на техните маси и на обратния квадрат на тяхното разделяне:
Но повечето от обектите не са точкови частици. За да намерите гравитацията между триизмерни обекти, трябва да ги разглеждате като точки в пространството. За симетрични форми като сфера намирането на тази точка е лесно.
теорема за черупката
Изложено е от Исак Нютон, който казва:
- Сферично симетричен обект влияе върху други тела чрез гравитация, тъй като цялата му маса е концентрирана в централната част.
- Ако обектът действа като сферично симетрична обвивка, тогава общата гравитационна сила е равна на нула.
Силата се счита за векторна величина, така че векторното сумиране на всички части на сферата е общата сила, която е еквивалентна на едно измерване на силата, взета от централната част. Следователно, когато се търси гравитация в топка от 10 kg, измерването се взема от центъра.
Сферата трябва да се възприема като набор от безкрайно тънки концентрични сферични черупки (лучени пръстени), така че силата вътре в нея е непрекъсната и зависи само от масата на сферата вътре в радиуса.
Има две ситуации, които трябва да имате предвид, когато изследвате гравитацията: кухо сферично тяло и твърда сфера.
№1 Куха сферична обвивка
Гравитацията действа като векторна добавка на гравитационните сили, действащи върху всяка част от черупката, и се равнява на нула. Маса m в сферично симетрична обвивка с маса M няма да изпитва никаква обща сила.
Нетната гравитационна сила е векторната сума на гравитационните сили, упражнявани от всяка част на черупката върху външния обект, сякаш цялата маса е концентрирана в центъра на сферата.
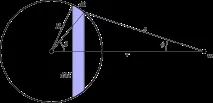
Тази диаграма описва геометрията за доказателството на теоремата за черупката. Сферична обвивка с маса M (вляво) е засегната от външна сила върху маса m (вдясно). Повърхностна площ на тънък срез от сфера, показана в цвят
№ 2 Твърда хомогенна сфера
Масата M и радиусът R влияят върху масата m при радиус d вътре в сферата. Приносът на всички обвивки на сферата към радиуса, по-голям от d от центъра на масата на сферата, може да бъде пропуснат. Само масата на сферата в определен радиус M d е важна и може да се разглежда като точка в центъра. Гравитацията ще бъде:
къде можеш да кажеш това
, където (p е плътността на масата на сферата).
Следователно в крайна сметка получаваме:
Виждаме, че масата m изпитва сила, линейно пропорционална на нейното разстояние (d) от центъра на масата на сферата.
Чистата гравитация в твърда сфера отразява векторната сума на гравитационните сили, действащи от всяка черупка върху външен обект. Получената нетна гравитация действа така, сякаш масата M е концентрирана в точка в центъра на сферата.