Хидравлика на подземни води (филтриране)
XI. ПОДЗЕМНА ХИДРАВЛИКА.
11.1. Основни понятия.
Филтрацията е явлението движение на водата в порите на почвата.
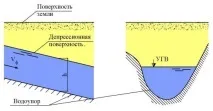
Водата, проникваща в почвата, се задържа на определена дълбочина от слой водоустойчива почва (плътна глина, скала) - водопровод и се движи по повърхността му. В този случай водопроводът служи като канал за земния поток. Подземният поток се движи, образувайки свободна повърхност, във всяка точка от която налягането е равно на атмосферното. Свободната повърхност на подземния поток се нарича депресионна повърхност.
Ориз. 11.1. Схема на безнапорния филтрационен поток. Еднообразно движение.
Начинът на движение на подземните води в пясъците и водопропускливите глинести почви е ламинарен. Турбулентно движение възниква само в едрозърнести почви (чакъл, камъчета).
Неравномерното движение на подпочвените води възниква в канали с неправилна форма, в случай на наклон на дъното на канала i ≤ 0 и в други случаи.
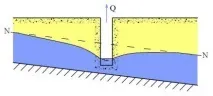
Например, неравномерно движение на подпочвените води се наблюдава при водовземане от изкоп, при поддържане на постоянна дълбочина в изкопа.
Ориз. 11.2. Схема на безнапорния филтрационен поток. Неравномерно движение.
При решаването на проблемите на хидравликата на подземните води те се занимават главно с въпросите за изграждане на депресионни повърхности и определяне на стойността на инфузионния поток. Освен това такива проблеми често се разглеждат в двумерна формулировка, свеждайки ги до така наречения „плосък“ проблем. За да се премине към равнинен проблем, се разглежда само част от филтриращия поток с единична ширина. От целия поток се отделя тънка негова част, за която се съставят уравнения. Според характеристиките на тази част от потока, получени в процеса на решаване на уравненията, те съставят картина на цялотофилтрационен поток.
В рамките на „плоския“ проблем потокът с единична ширина се характеризира със стойността на специфичния дебит на филтриране q, т.е. дебитът на единица широчина на потока.
Q е общият дебит на филтриращия поток, ê é
b е ширината на канала на филтриращия поток, [m].

Ориз. 11.3. „Плоска“ задача
Забележка: при изчисляване на специфичния филтрационен поток считаме, че каналът е цилиндричен, освен това с правилна форма. Това се прави като приближение за преход към "плоска" задача. Всеки канал с различна степен на точност може да бъде представен в тази форма. В бъдеще ще приемем, че каналът на филтриращия поток е достатъчно широк и такова приближение е оправдано.
Пренебрегване на скоростта.
Поради малките скорости на филтрационните потоци, при съставяне на уравнението на Бернули за такива потоци стойността на скоростния напор се счита за равна на нула. (Това изобщо не означава, че скоростите на потока в този случай се считат за постоянни. От пренебрегването на налягането на скоростта следва, че промяната в скоростта на филтриращия поток не допринася за енергийните характеристики на този поток и следователно промяната в скоростта не влияе на характеристиките на движение.)
По този начин общият напор и потенциалният напор са равни.
H = H общ = H потенциал = ρ p g + z .
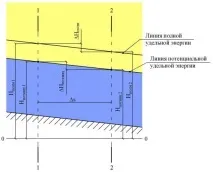
Освен това ще обозначим такъв напор на филтриращия поток като H, като вземем предвид казаното по-горе за пренебрегването на скоростния напор.
Съответно хидравличният наклон и пиезометричният наклон стават идентични.