Хистограми
Лаборатория №6
Хистограми
Хистограмата е поредица от ленти с еднаква ширина, но различна височина, която показва разсейването и разпределението на данните. Ширината на колоната е интервал в обхвата на наблюденията, височината е количеството данни на интервал, т.е. честота . По същество хистограмата показва разпределението на изследвания показател. Хистограмата ви позволява да оцените естеството на разпространението на индикатора и да разберете къде да насочите усилията за подобряване.
Характерни видове хистограми са показани на фиг. 6.1.
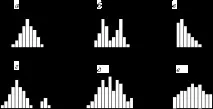 |
Фиг. 6.1. Типични видове хистограми
На фиг. 6.1а показва обичайния тип хистограма с двустранна симетрия, което показва стабилността на процеса.
На фигура 6.1, b има два пика в разпределението (двугърба хистограма). Такава хистограма се получава чрез комбиниране на две разпределения, например в случай на два вида суровини, промяна на настройката на процеса или комбиниране в една партида от продукти, обработвани на две различни машини. Необходимо е разделяне на продукта.
На фиг. 6.1c показва хистограма с прекъсване. Такова разпределение се получава, когато е невъзможно да се получи стойност под (или над) някаква стойност. Подобно разпределение има и когато всички продукти с показател под (и/или над) нормата са изключени от партидата, т.е. първоначално беше партида с голям брой дефектни продукти. Същото разпределение се получава, когато измервателните уреди са били дефектни.
На фиг. 6.1d показва хистограма с остров. Получава се, когато има грешки в измерванията или когато определено количество дефектни продукти се смесват с добри.
На фиг. 6.1, д показва хистограма с пропуски ("гребен"). Оказва се, когато ширинатаинтервалът не е кратен на мерната единица или в случай на грешки на оператора.
На фиг. 6.1, д показва хистограма под формата на плато. Получава се, когато се комбинират няколко разпределения с малка разлика в средните. В този случай е необходимо наслояване.
Пример 6.1. Разкрийте естеството на дисперсията на индекса на качеството на продуктите, изработени от метален материал.
За да определим естеството на дисперсията на индикатора, изграждаме хистограма.
Редът на изобразяване на хистограмата:
1. Очертаваме индикатора за качество, който ще бъде изследван. В този случай това е коефициентът на деформация на материала.
2. Извършваме измервания. Трябва да има поне 30 ... 50 данни, оптимално - около 100.
Резултатите от измерванията на коефициента на деформация са представени в табл. 6.1.
Резултатите от измерването се въвеждат в електронна таблица. В клетка A1 въведете заглавието на произведението. Започвайки от клетка A3, въведете серийните номера на измерванията от 1 до 100 в колоната, например, като използвате командата Edit 4 Fill 4 Progression .... В клетки B3:B102 въвеждаме стойностите на коефициента на деформация от таблицата. 6.1.
1. Въведете мерната единица. Мерната единица е равна на точността, с която са направени измерванията, в този случай 0,1. Въведете мерната единица в клетка E2.
4 . Намираме минималните и максималните стойности на извадката. Минималните и максималните стойности на извадката се намират с помощта на статистическите функции MIN и MAX, съответно, в клетки E3 и E4. В този случай интервалът за тези функции е посочен от клетка B3 до клетка B102.
5. Намираме обхвата на извадката в клетка E5 като разликата между максималните и минималните стойности на извадката.
6. Определяме предварителния брой интервали Kprev като корен квадратен от размера на извадката N. Броят на интервалите се намира в клетка E6. Тъй като броят на интервалите трябвае цяло число, т.е. полученият квадратен корен трябва да бъде закръглен до цяло число, след което първо в клетка E6 въвеждаме математическата функция ROUND. В реда Брой цифри на тази функция посочваме 0, защото трябва да се закръгли до цяло число. След това преместваме курсора на реда Number и като аргумент на функцията ROUND вграждаме функцията ROOT. За да направите това, отворете списъка с функции в лентата с формули, изберете Други функции ... и отворете математическата функция ROOT. Като аргумент на функцията ROOT, отново чрез списъка в лентата с формули, избираме статистическата функция COUNT, като аргумент на която въвеждаме диапазон от клетки от B3 до B102. Тъй като функцията COUNT отчита броя на числата в посочения диапазон, т.е. в този случай размерът на извадката, тогава ще се получи стойността 100. Тогава функцията ROOT ще преизчисли тази стойност до 10, а функцията ROUND ще я закръгли до цели числа, т.е. до 10. Като цяло формулата в клетка E6 ще изглежда така: =ROUND(ROOT(COUNT(B3:B102)),0)
7. Определяме ширината на интервала в клетка E7 с помощта на формулата h = R / K prev закръглена до най-близката мерна единица, т.е. в нашия случай до десети. Формулата в клетка E7 ще изглежда така: =ROUND(E5/E6;1).
8 . Въведете числата на интервалите. За да направите това, в клетка D 9 въведете заглавието на колоната номер int. Започвайки от клетка D 10, въведете интервалните числа от 1 до около 25.
9. Изчисляваме границите и средните точки на интервалите. В клетка E10 изчисляваме долната граница на първия интервал, използвайки формулата
За да направите това, въведете формулата =E3-E2/2 в клетка E10 и вземете стойността на долната граница на първия интервал 0,05.
В клетка G 10 изчисляваме средната стойност на първия интервал, например, като използваме статистическата формула AVERAGE. Копираме получената формула в диапазона G 11: G 34.
Тъй като вече в десетиинтервал, долната граница е 1,85. което е по-голямо от Xmax, тогава необходимият брой интервали е 9. Следователно съдържанието на клетките в диапазона D 19: F 34 трябва да бъде изчистено.
Резултатите от изчислението са показани на фиг. 6.1.
 |
Фиг.6.1. Изчисляване на данни за изграждане на хистограма в пример 6.1.
Готовата хистограма е показана на фиг. 6.2, а.
Възможно е хистограмата да се представи като непрекъсната крива или прекъсната линия. За да направите това, отворете контекстното меню в областта на хистограмата, изберете командата Chart type…, изберете Scatter chart и съответния й тип. (Фиг. 6.2, b, c).
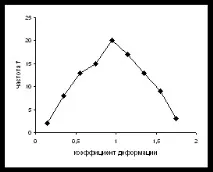
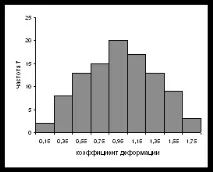
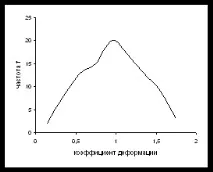
Фиг. 6.2. Хистограма под формата на стълбовидна диаграма (a), прекъсната линия (b)
и непрекъсната крива (c).
Получената хистограма е близка до конвенционалната хистограма с двустранна симетрия, което показва стабилността на процеса.
1. Извършете изчисления и конструкции в съответствие с пример 6.1.
2. Изградете хистограма въз основа на резултатите от измерването на дължината на частите, mm (Таблица 6.2). Какви мерки са необходими за стабилизиране на технологичния процес?