III. Диференциално смятане

През 17-18 век в математиката се появяват два най-мощни метода за изследване на свойствата на функция:

Диференциално и интегрално смятане, чиито основатели са английският учен Нютон и немският учен Лайбниц.

Основната концепция на диференциалното смятане е концепцията за производната на функция. Някои практически задачи от различни области на знанието доведоха до тази концепция. Нека разгледаме някои от тях.

§1. Проблеми, водещи до понятието производна на функция.

а) Проблемът за скоростта на неравномерно праволинейно движение (физическо)

Нека материалната точка се движи по права линия, започвайки от точка 0, неравномерно. За време t ще измине някакъв път S, т.е. S= (t) - уравнение на движението. Изминатото разстояние варира с времето. Каква е скоростта на тази промяна?

Тъй като движението е неравномерно, обичайното разбиране за скорост тук е неприемливо. Тук характеристиката на движението е моментната скорост, скоростта в дадена точка.

Ние аргументираме следното: нека в някакъв момент от времето t0 тялото вече е преминало пътя S0=(t0) и е било в точка M0, а в някакъв друг момент от времето

е преминало пътя S =S0+ S и е в точка M. През интервала от време t точката е преминала пътя S = S -S0=(t) -(t0)=( t0 + t)- (t0) .

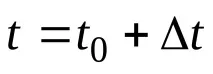
Ако направим съотношението

S/t, то ще даде средната скорост на точката за времетоt

Vav=

S/t = (( t0 + t)- (t0))/ t; (1)

Средната скорост не може да отразява всички колебания в скоростта на движение, тя ги изглажда.

За да разберете по-точно действителната скорост на движение в даден момент t, трябва да вземете по-малък интервал от време t.

Границата на отношението

S/t при t0 се наричаскорост на движение в даден момент t0.

По този начин, за да се намери скоростта на точка в даден момент от време, човек трябва да може да намери граница на формата (2).

б) Задачата за допирателна към крива (геометрична).

T

Нека първо да дадем самата дефиниция на допирателна към крива в дадена точка. Нека има дадена крива L и точка M0 върху нея. Вземете друга точка M върху L и начертайте секуща M0M. Когато промените позицията на точка M върху кривата L, позицията на секанса също ще се промени. Ако при неограничен подход на точка M по протежение на кривата до точка M0c от която и да е страна, секансът M0M има тенденция да заеме позицията на определена права линия M0T, тогава тази линия M0T се нарича допирателна към кривата L в точка M0.

---