Итеративни методи - 3D триангулация
Методи, базирани на критерия на Делоне
Първо, нека си припомним какво представлява критерият на Делоне. Казва се, че триъгълна решетка в равнина удовлетворява критерия на Делоне (или е триангулация на Делоне), ако никакви други възли на тази мрежа не попадат в окръжността, описана около всеки триъгълник [7].
Триангулацията на Делоне има редица интересни свойства [7, 8]. По-специално, триангулацията на Делоне има най-голямата сума от минималните ъгли на всички нейни триъгълници, както и най-малката сума от радиуси на окръжности, описани около триъгълници сред всички възможни мрежи в една и съща точкова система (Фигура 2.15).
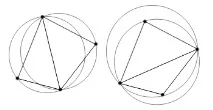
Фигура 2.15 - Решетка, която удовлетворява критерия на Delaunay (вляво) и не го удовлетворява (вдясно)
При опит да се обобщят идеите на алгоритмите за случая на три измерения бяха открити редица проблеми. Първо, критерият на Делоне не работи в 3D случай в смисъл, че мрежа, която удовлетворява критерия на Делоне, не максимизира минималните ъгли. Второ, алгоритмите за последователно подобрение също не работят в космоса. Нека се спрем на това по-подробно.
В 2D намаляването на произволна триангулация до триангулация на Делоне се постига чрез пренареждане на вътрешния ръб на четириъгълника, образуван от триъгълниците. Операцията (т.нар. "обръщане", от английски flip) продължава итеративно за всяка двойка триъгълници, които не отговарят на критерия, докато останат такива триъгълници.
2D "обръщането" също има 3D аналог, макар и базиран на различна идея. Почти всеки два съседни тетраедъра могат да бъдат превърнати в три. За да направите това, достатъчно е да вмъкнете вътрешен ръб вътре в шестоъгълника, образуван от тетраедри (Фигура 2.16), и това може да стане по уникален начин. Думата "почти"стои тук, защото ако всеки три върха на този шестоъгълник лежат на една и съща права или четири от неговите върхове лежат в една и съща равнина, тогава тази операция ще доведе до образуването на изродени тетраедри. Операцията по замяна на 2 тетраедъра с 3 и обратно се нарича "търговия" (от английски trade) [3].
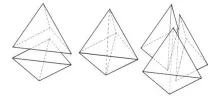
Фигура 2.16 - "Търговия" - замяна на 2 тетраедъра с 3
Опитите да се използва "търговия", за да се приведе произволна триизмерна мрежа към триангулацията на Delaunay, завършиха неуспешно, тъй като такива алгоритми много често се завъртаха в локални оптимуми. В същото време важен теоретичен резултат беше получен не толкова отдавна: канадският математик Б. Джо (Бари Джо) доказа, че ако се добавят нови тетраедри към вече съществуваща триангулация на Делоне (чрез разделяне на един от вътрешните или чрез прикрепване на тетраедър към външно лице), тогава получената мрежа може да бъде гарантирано редуцирана до триангулация на Делоне, използвайки последователни „сделки“ [9]. Този факт играе огромна роля при конструирането на ограничени триангулации на Делоне.
Общ недостатък на всички методи, базирани на критерия на Delaunay, е изключително високата чувствителност към точността на машинните изчисления. Много изчислителни процедури, използвани в тези методи (намиране на центъра и радиуса на описаната окръжност, проверка на копланарността и колинеарността на векторите и т.н.) са лошо обусловени проблеми и тяхната неизбежна интензивна употреба също така неизбежно води до натрупване на грешки при закръгляване, което в крайна сметка може да доведе до грешки в мрежовата структура или зацикляне на алгоритъма [3].
Частично решение на този проблем може да бъде използването на числови типове с фиксирана запетая. Поради отделното съхранение в 24-байтовата структура на целите и десетичните части на числото (под формата на цели числа), по-горе е лошоусловни задачи, е възможно да се постигне точност до 10 знака след десетичната запетая, което вече е повече или по-малко приемлив резултат [5].
Недостатъкът на този подход е (много значително) намаляване на изчислителната скорост. Следователно всички тези операции трябва да се изпълняват на ниво подпрограми, което води до допълнителни разходи за ресурси.
Общата идея на този клас методи е последователно да се премахват фрагменти с тетраедрична форма от даден регион, докато целият регион бъде „изчерпан“. Въпреки това, този лесно въобразим процес всъщност няма много общо с практическото прилагане. Английското наименование "advancing front" (което може да се преведе като "напредване на фронта") може би по-добре отразява същността на алгоритмите.
Отправната точка на всички алгоритми от този клас е определена триангулация на границата на дадена област, а не груба, но най-пълно съответстваща на изискванията на разработчика, тъй като няма да има допълнителни промени в тази триангулация. Ако е необходимо да се осигури съгласуване на триангулацията в сложна област или ако триангулацията на повърхността е зададена първоначално, тогава използването на метода на изчерпване ще бъде най-добрият избор.
Граничната триангулация е самият „фронт“, споменат в заглавието. Използвайки всеки триъгълник отпред, е възможно да се изгради тетраедър на неговата основа, а четвъртият връх на тетраедъра може да бъде или друг връх на предната страна, или допълнителен възел, поставен вътре в дадената област. При премахване на получения тетраедър отпред, от 1 (в случай на вмъкване на допълнителен възел) до 4 лица могат да бъдат премахнати и от 1 до 3 нови лица могат да бъдат добавени едновременно. По този начин настоящият фронт на вземане на проби постепенно се придвижва напред в пространството - оттук и името"настъпващ фронт". Като актуализирате данните от предната страна, можете отново да премахнете тетраедъра, да актуализирате отново предната част и така нататък, докато цялата област бъде "изчерпана".
Въпреки привидната простота на идеята, прилагането на алгоритъма за изчерпване е изпълнено с редица тънкости (имайте предвид, че прилагането на алгоритми за изчерпване в двумерния случай е много по-просто). Най-трудната част от всеки алгоритъм за изчерпване е да се провери коректността на конструирания тетраедър, защото е необходимо да се уверите, че този нов тетраедър не се пресича с нито един съществуващ. Освен това при всяка итерация на алгоритъма тази процедура с различни параметри може да бъде извикана от 5 до 20 пъти (понякога повече). Ефективността на алгоритъма зависи главно от това как се изпълнява тази проверка.
Втората трудна точка е крайъгълният проблем на 3D дискретизацията. Не е необичайно в резултат на работата на алгоритъма да се формират области, които не могат да бъдат дискретизирани без използване на допълнителни вътрешни възли (в плоския случай всеки многоъгълник може да бъде разделен на триъгълници само с вътрешни ръбове).
Също така си струва да запомните, че по време на работа на алгоритъма предната част може да се разпадне на несвързани фрагменти.
Четвъртата характеристика на алгоритмите за изчерпване е необходимостта да се контролира обемът и/или линейните размери на получените тетраедри [3].
1.3 Характеристики на свързването в сложни зони
Един общ проблем с дискретизацията е триангулацията на сложни домейни, т.е. зони, обект на различни допълнителни ограничения, дължащи се например на промени в свойствата на материала [1].
Условно могат да се разграничат два вида комплексни зони:
1) области, състоящи се от непресичащи сезатворени поддомейни (Фигура 2.17);
2) области с вътрешни ограничения под формата на повърхности или криви (Фигура 2.18).
Пример за областта на първия тип е моделът на композитни материали, пример за втория тип са моделите, изследващи развитието на пукнатини в материала.
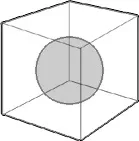  |
Фигура 2.17 - Пример за сложна зона от тип I: топка в куб (композитен материал)
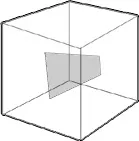
Фигура 2.18 - Пример за сложна област тип II: фрагмент от равнина в куб
По същество дискретизацията на сложни региони от първия тип се състои в независима дискретизация на всеки подрегион с условието за съвпадение на мрежата на границите.
За сложни зони от втори тип обикновено се използват методи, базирани на критерия на Делоне или методи за корекция на границите [7, 9, 10]. Тези методи, с някои допълнителни условия, могат да се използват и за дискретизиране на региони от първия тип.
1.4 Оценка на качеството на мрежата
Сравнението на ефективността на различните методи за дискретизация е невъзможно без определяне на определен критерий за качество на изградената мрежа. Тъй като мрежата е изградена не в името на самата конструкция, а в името на решаването на някакъв проблем, разумно е този критерий да се свърже с апроксимационните свойства на мрежата. Според теорията тези свойства зависят главно от формата на елементите [10]. Оптимална от гледна точка на точност и удобство на намиране е следната оценка [11]:
където е обемът на тетраедъра и е най-големият от продуктите на дължините на тройката ръбове, излизащи от един връх. По-нататък ще използваме тази оценка.
Тъй като стойността, получена от формула (2.4), е от порядъка на десети и стотни, за по-голяма яснота е удобно да се посочи стойността на идеалния случай - правилен тетраедър. (За него, както можете да изчислите, тази стойност е равна на ). Да се обадимтова е съотношението на "апроксимационната характеристика" (AR) на елемента. Възможните стойности на AH са в диапазона от 0 до 1; колкото по-близо до 1, толкова по-добре.
За качествен анализ на мрежата минималните и средните стойности на AC са от най-голямо значение: първата участва в оценката на качеството на приближението, втората показва общото качество на мрежата. За геометрично сложни области добър резултат ще бъде средна стойност на AX, равна на поне 1/2. [12]
Има и други критерии за оценка на качеството на елементите на мрежата (Таблица 2.1)
Таблица 2.1 - Критерии за оценка на качеството на мрежестите елементи