ИЗЧИСЛЯВАНЕ НА ЕЛЕМЕНТИ НА ЕКВИВАЛЕНТЕН АКТИВЕН И ПАСИВЕН ЧЕТИРИПОЛЮСЕН, Изчисляване на еквивалент
Изчисляване на еквивалентния четириполюсник
Съгласно заданието ни е дадена еквивалентна четириклемна мрежа (фиг. 6.1), за която е необходимо да се определят съпротивителните елементи Z1, Z2, Z3 и Z4 и техните стойности.
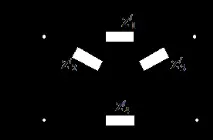
За определяне на Z/1, Z/2, Z/3 и Z/4 използваме А-параметрите на изследвания четириполюсник ((3.6) (3.9)) и еквивалентния четириполюсник ((6.1) - (6.4)), както и израз (6.5).
където i и j са индексите на A-параметрите.
Още от изразите на A-параметрите, написани за мостовия четириполюсник, става ясно, че няма смисъл да се определят и изчисляват елементите за еквивалентния четириполюсник, посочен в задачата, тъй като (съдейки по изразите (6.1) (6.4)) той ще има повече елементи от разглеждания.
Изчисляване на елементите на еквивалентна активна четирикрайна мрежа
Има няколко начина за изграждане на активен четириполюсник:
1) замяна на капацитети с честотно зависими отрицателни съпротивления;
2) замяна на индуктивности с жиратори (входното им съпротивление е обратно на съпротивлението на товара);
3) каскадно свързване на прости мрежи с четири порта.
Нека изградим еквивалентна активна мрежа с четири терминала от каскадно свързване на по-прости. За целта използваме системната функция H(S) (3.15) и я разглеждаме като трансферна функция H(p).
Нека намерим корените на знаменателя на израз (6.6) и запишем трансферната функция H(p) във формата:
Нормализираме H1(p) с коефициента , и в резултат получаваме
където a = 1,02 и b = 0,601.
Това е блокиращ филтър.
Принципна диаграма на такъв филтър е показана на фиг. 6.2.
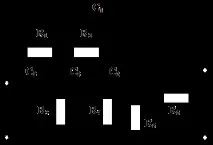
Филтърът за прихващане се изчислява съгласно следнотопоследователности:
1) изберете С1 = , (6.9)
2) задайте С3 = С4 = , (6.10)
3) изчисляване = ,(6.11)
4) задайте R3 = и R1 = R2 = 2R3, (6.12)
5) изберете , (капацитетът C2 може да бъде равен на нула), (6.13)
6) изчисляване, (6.14)
7) изчисляване, (6.15)
8) определя .(6.16)
Придържайки се към горната последователност, ще изчислим елементите на първата каскада.
1. Нека изберем C1 = 2 F.
4. Тогава R3 = Ohm и R1 = R2 = 20,4951 = 0,99 Ohm.
5. . Така че избираме C2 = 0,1 F.
Така имаме следните количества:
C1 = 2 F, C2 = 0,1 F, C3 = 1 F, R1 = R2 = 0,99 ома, R3 = 0,4951 ома, R4 = 11,222 ома.
Денормализираме капацитетите по честота с коефициента , в резултат на което получаваме, че:
C1 = 90,35 uF, C2 = 4,52 uF, C3 = 45,2 uF.
Сега денормализираме всички елементи с коефициент 10000, в резултат на което получаваме, че:
C1 = 9,035 nF, C2 = 0,452 nF, C3 = 4,52 nF, R1 = R2 = 9,9 kOhm, R3 = 4,951 kOhm, R4 = 112,22 kOhm.
За прилагане на коефициента k = 1.831 използваме неинвертираща усилвателна верига, за която изчисляваме R5 и R6 съгласно (6.17).
където е делителя на напрежението на изхода на операционния усилвател.
Избираме R6 = 10 kOhm, след това R5 = 8,31 kOhm.
Схема на първата каскада
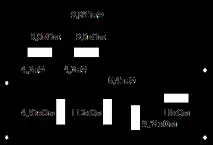
Нормализираме H1(p) с коефициента , и в резултат получаваме
където a = 0,772 и b = 0.
Това е блокиращ филтър.
Принципна диаграма на такъв филтър е показана на фиг. 6.2.
Придържайки се към горната последователност от изрази (6.9) (6.16), ще изчислим елементите на втората каскада.
1. Нека изберем C1 = 2 F.
4. Тогава R3 = Ohm и R1 = R2 = 20,569 = 1,138 Ohm.
5. . Така че избираме C2 = 0 F.
По този начин имамеследните количества:
C1 = 2 F, C2 = 0 F, C3 = 1 F, R1 = R2 = 1,138 ома, R3 = 0,569 ома, R4 = 7,71 ома.
Денормализираме капацитетите по честота с коефициента , в резултат на което получаваме, че:
C1 = 86,07 uF, C2 = 0 uF, C3 = 43,03 uF.
Сега денормализираме всички елементи с коефициент 10000, в резултат на което получаваме, че:
C1 = 8,607 nF, C2 = 0 nF, C3 = 4,3 nF, R1 = R2 = 11,38 kOhm, R3 = 5,69 kOhm, R4 = 77,1 kOhm.
За прилагане на коефициента k = 2.148 използваме неинвертираща усилвателна верига, за която изчисляваме R5 и R6 съгласно (6.17)
Избираме R6 = 10 kOhm, след това R5 = 11,48 kOhm.
Схема на втората каскада

Това е RC верига, чиято електрическа схема е показана на фигура 6.5.
Схема на елемента на RC верига
Такава верига се изчислява по следния начин.
Записваме A-параметрите (6.18) за веригата (Фигура 6.5).
След това записваме системната функция за четириполюсника (фиг. 6.5), използвайки израз (3.14) и A-параметри. След някои математически трансформации получаваме
Може да се види, че системната функция, записана в този израз, е подобна на външен вид на H3(p). Тогава можем да напишем система с две уравнения с две неизвестни.
Решавайки горната система, получаваме стойността на елементите:
R = 112,58 ома и C = 43,538 nF.
Елементна схема на третия етап
Еквивалентна активна мрежа с четири терминала се получава след каскадно свързване на RC вериги, обсъдени по-горе, и схеми на операционен усилвател. Показано е на фиг. 6.6.