ИЗЧИСЛЯВАНЕ НА РЕЖИМА НА ЕЛЕКТРИЧЕСКАТА МРЕЖА С ДВУСТРАННО ЗАХРАНВАНЕ, КАТО СЕ ОТЧИТА ТЕМПЕРАТУРНАТА ЗАВИСИМОСТ
Изчисляването на стационарни условия е една от основните задачи, които трябва да бъдат решени при проектирането и експлоатацията на електрическите мрежи. Стандартните математически модели отчитат нелинейността, въведена от потребителите на енергия, но параметрите на еквивалентната верига на електрическата мрежа обикновено се задават в линейна форма. В същото време тези параметри се характеризират и с различни видове нелинейност, сред които най-важна е температурната зависимост на активните съпротивления на надлъжните клонове.
Понастоящем основната област на отчитане на този фактор в електроенергетиката е изчисляването на загубите на енергия. Температурната зависимост на съпротивлението обаче обикновено се взема предвид само на етапа на изчисляване на загубите като функция на токовете или предаваните мощности; самите токове и мощности в повечето случаи се определят без оглед на температурата. Тази разпоредба се дължи на факта, че ако загубите на натоварване са правопропорционални на активните съпротивления, тогава за токове и мощности активните съпротивления на мрежовите елементи са по-малко значим фактор, често считан за второстепенен. Всъщност еквивалентните вериги на електрическите мрежи съдържат не само активни, но и индуктивни съпротивления, като последните в много случаи преобладават. Освен това, ако мрежата е отворена, тогава разпределението на потока обикновено зависи малко от параметрите на мрежовите елементи и се определя главно от натоварванията.
Независимо от това, функционалните връзки между режимните параметри на електрическите системи са сложни и нелинейни и е доста трудно да се предвиди степента на влияние на отделните фактори върху резултатите от изчислението във всяка конкретна ситуация. Поради това съществуват разработки в областта на отчитане на температурната зависимост на съпротивленията при изчисляване на режимите [9, 2, 5-7].
Тази статия също така предлагаедно от решенията на този проблем. Температурата се определя въз основа на уточнените уравнения на топлинния баланс на въздушните линии, като се вземе предвид слънчевата радиация. В същото време като обект на изчисления беше избрана мрежа с двупосочна мощност. Този избор се дължи на факта, че в затворените мрежи, за разлика от отворените мрежи, съпротивленията на елементите имат основно влияние върху разпределението на потока. Освен това, когато активните съпротивления се променят, степента на хомогенност на мрежата се променя, което трябва пряко да повлияе на големината на загубите на енергия.
1. Математически модели. Двупосочна електрическа мрежа и нейната еквивалентна схема са показани на фиг. 1, 2. Математическият модел на стационарното състояние, като се вземе предвид температурната зависимост на съпротивленията, може да се запише в следната форма:
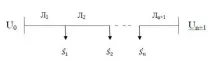
Ориз . 1. Мрежа с двупосочно захранване
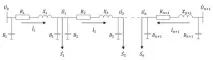
Ориз. 2. Резервна верига

където Ui, δi са модули на напрежение и фази във възлите, kV и rad; Pн,i, Qн,i – мощности на потребителите, MW и Mvar, при условие че напрежението в съответния възел е Uном, kV; a2,i, a1,i, a0,i, b2,i, b1,i, b0,i – коефициенти на квадратична апроксимация на статичните характеристики на активната и реактивната мощност на напреженови товари; li е дължината на линията, km; nц,i и nф,i са броят на линейните вериги и броят на проводниците във фазата; dpr,i – диаметър на телта, m; αvy,i – коефициент на топлопреминаване на проводника (чрез принудителна конвекция), W/(m2∙°C); Θi, Θen – температура на проводника и околната среда, °C; Ti, Tamb - абсолютни температури на проводника и околната среда; εп и As са излъчвателната способност на повърхността на проводника и поглъщателната способност на повърхността за слънчева радиация; C0 = 5.67∙10-8 W/(m2∙K4) – константа на Стефан-Болцман: qsun,i – плътност на потока слънчева радиация на повърхносттапроводници, W/m2; R0,i – активно съпротивление на линията, Ohm, при 0 °C; α е температурният коефициент на съпротивление.
Уравнения (1), (2) са стандартни уравнения на възловото напрежение под формата на токов баланс в полярни координати. Собствената и взаимната проводимост на възлите са описани по отношение на съпротивленията и капацитивната проводимост на линиите. Това се прави с цел изрично включване в уравненията на нелинейни елементи - активни съпротивления.
В допълнение към уравненията на електрическия режим (1), (2), системата включва уравненията на топлинния баланс за въздушни линии (3). Първият член в тези уравнения е загубата на активна мощност в един проводник с дължина 1 m, изразена в [W]. За да преобразувате загубите в цялата линия в [MW] към определената стойност, използвайте множителя пред квадратната скоба. Изразът в квадратни скоби в разглеждания термин е квадратът на модула на спада на напрежението в линията. Вторият член определя топлинния поток от проводника, дължащ се на конвекция и топлинно излъчване, минус слънчевата радиация, записана по подобен начин [9].
Изрази (4) и (5) са формули за свързване на уравненията на електрически и топлинни режими, които определят температурната зависимост на активните съпротивления (4) и квадратите на общите съпротивления (5). Тези формули са изписани отделно само за яснота и за намаляване на нотацията на основните уравнения; всъщност при решаването на системата формули (4), (5) се заместват в уравнения (1), (2) и (3). В този случай общата размерност на системата става равна на (3n + 1), а в нея са неизвестни модулите и фазите на напреженията Ui, δi, както и температурите на проводниците Θi.
Характеристика и недостатък на този модел е множеството решения. И така, всяко от уравненията на топлинния баланс иманай-малко две реални решения и същият брой решения обикновено има нелинейна система от уравнения на електрическия режим (за дадени съпротивления). Тогава общият брой на решенията може да се оцени като 2(n+1)2 и само две от тях имат физически смисъл, докато останалите са чисти математически абстракции. За да се избегне това, може да се използва опростена форма на уравненията на топлинния баланс [9], която изключва „странни“ решения:
, (6)
(7)
(8)
(9)
Тук ΔΘd = Θdop - Θokr - превишаване на допустимата температура на проводника над температурата на околната среда; ΔP0,i са загубите на мощност в проводник с дължина 1 m, които биха възникнали при действителен ток и температура на проводника 0 °C [9]. Изразявайки тези загуби по отношение на модули и фази на напрежение, получаваме:
. (10)
Заменяйки уравнение (3) с (6), като вземем предвид (7)-(10), получаваме математически модел на режима, броят на решенията в който се намалява до две (ако системата от уравнения за възлови напрежения при постоянни съпротивления има 2 решения). Освен това и двете решения имат физически смисъл.
2. Избор на методи за решаване на системи от уравнения. При изчисляване на режимите на електрическите мрежи най-често се използва методът на Нютон. Естествено решение би било директно да се приложи същият метод към модел, който взема предвид температурата, например (1)-(5). Въпреки това уравненията на топлинния баланс се различават рязко от уравненията на възловото напрежение, в резултат на което може да се очаква влошаване на конвергенцията на изчислителния процес. По-специално, ако токовете са далеч от допустимите за отопление, тогава влиянието на температурата върху електрическия режим ще бъде слабо, което ще доведе до лоша условност на матрицата на Якоби (в частта, която съответства на уравненията на топлинния баланс и температурните производни).
Да сеЗа да се избегне това, алгоритъмът може да се основава на решението само на уравненията на възловите напрежения по метода на Нютон, а влиянието на температурата може да се вземе предвид като допълнителен изясняващ фактор. В този случай са възможни два подхода.
1. Организация на двоен итеративен процес: вътрешният цикъл е решението на уравненията на възловото напрежение; външният цикъл е температурно избистряне. Алгоритми от този вид са описани в трудовете на д-р, доц. Барсков В.В.
2. Уточняване на температурата при всяка итерация на метода на Нютон при следващото изчисляване на елементите на якобиевата матрица. С други думи, температурната корекция се въвежда "вътре" в метода на Нютон.
Общото описание и характеристиките на разглежданите методи са обобщени в (Таблица 1).
Числени методи за изчисляване на мрежовия режим с отчитане на температурата
Съвместно решаване на уравнения
Двоен итеративен процес
Корекция на вътрешна температура
Уравненията на възловото напрежение и топлинния баланс се решават като една система по метода на Нютон.
1. Задаване на първоначалните температурни приближения.
2. Изчисляване на активни съпротивления.
3. Решаване на уравнения на възлови напрежения по метода на Нютон.
4. Изчисляване на следващите температурни приближения и връщане към точка 2.
При всяка итерация на решаване на уравненията на възловото напрежение по метода на Нютон, температурите и активните съпротивления се прецизират чрез решаване на уравненията на топлинния баланс. В този случай елементите на матрицата на Якоби и десните части на линеаризираните уравнения на възловите напрежения се изчисляват, като се вземат предвид промените в активните съпротивления.
Якобиев матричен ред
Всеки от тези методи по принцип може да се използва както за модела без опростявания (1)-(5), така и за модела с квадратична апроксимация (1), (2), (4)-(10). Въпреки това, съвместното решение по метода на Нютонуравнения (1), (2), (4)-(10) вместо (1)-(5) води не до опростяване, а до усложняване на изчисленията, тъй като въпреки приближението системата все още остава нелинейна и температурата се определя от по-тромави изрази. В същото време при другите два метода изчисляването на температурите е отделено в отделна изчислителна процедура. Следователно използването на квадратично приближение в тези случаи води до значително намаляване на обема на изчисленията: температурите се определят аналитично, а не числено. В този случай практически няма загуба на точност [9].
По този начин е препоръчително да се използва методът на съвместно решаване на уравнения за модела без опростявания, а методът на корекция на вътрешната температура - за модела с квадратично приближение.
По-долу са резултатите от съответните изчисления. В този случай, въпреки че методът на двойния итеративен процес може да се използва и за модел с квадратично приближение, при сравнителни изчисления беше използван модел с опростени уравнения на топлинния баланс [4]. Това не влияе на конвергенцията, но дава възможност допълнително да се оцени влиянието на точността на уравненията върху резултатите от изчисляването на режимите.
3. Анализ на резултатите. За сравняване на методите помежду си, както и с класическия метод, който не отчита температурата, бяха разгледани четири характерни режима (таблици 2, 3) на мрежа с три линии (n = 2).
Характеристики на режими, дължини на линии и марки проводници