Изграждане на правилен многоъгълник отстрани (с помощта на - Изображение 191024-7
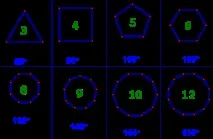
Построяване на правилен многоъгълник по неговата страна (чрез ротация) Многоъгълникът се нарича правилен, ако всички страни са равни и всички ъгли са равни. Първо трябва да изчислите вътрешния ъгъл на правилен многоъгълник. От училищния си курс по геометрия знаете (или ще разберете малко по-късно), че сумата от ъглите на изпъкнал n-ъгълник е 180o(n - 2). Въз основа на тази теорема е лесно да се изчисли стойността на вътрешния ъгъл на правилен многоъгълник. Таблицата по-долу показва сумите от ъгли и вътрешни ъгли за някои правилни многоъгълници. Познавайки стойността на вътрешния ъгъл на правилен многоъгълник, няма да е трудно да се конструира самият многоъгълник. Нека построим две точки - два съседни върха на многоъгълника. Нека маркираме една от точките като център на въртене, изберете втората точка и я завъртете във вътрешния ъгъл. В резултат на това ще бъде изграден третият връх на многоъгълника. Маркираме новопостроената точка като център на въртене и завъртаме съседния връх (бивш център) към вътрешния ъгъл. Четвъртият връх ще бъде изграден. Третата стъпка ще се повтаря, докато не бъдат построени всички върхове на многоъгълника. Свържете последователно върховете на многоъгълника със сегменти.
Снимка 7 от презентация "Построяване на някои правилни многоъгълници"
Размери: 472 x 309 пиксела, формат: png. За да изтеглите безплатно картина за урок по геометрия, щракнете с десния бутон върху изображението и щракнете върху „Запазване на изображението като. ". За да покажете снимки в урока, можете също да изтеглите презентацията „Изграждане на някои правилниpolygons.pptx" с всички снимки в zip архива. Размер на архива - 1042 KB.
Подобни презентации
„Правилни многоъгълници на задачата” – Индивидуална задача. Страна на правилен многоъгълник. Попълнете празните клетки на таблицата (страна на многоъгълника). Как да се оценя в клас? Вписана и описана окръжност. Сборът от всички ъгли на n-ъгълник е равен. Тест (20 задачи с един верен отговор). Оценете себе си. Двоичен тест. В двора на нашето училище има квадратна цветна леха.
„Площ на многоъгълник“ - Площта на фигурата (многоъгълник). Площта на многоъгълника. Площ на правоъгълник и успоредник. Еднаквите многоъгълници имат равни площи. Srhombus = ах. Изчислете площта на ромб, чийто диагонали са 6 и 8 см. Свойство № 2. Каква е площта на боядисаната повърхност? Stтриъгълник=1/2(ah). Подгряваща задача 2.
"Правилни многоъгълници 9 клас" - Построяване на правилен петоъгълник 2 начина. Удвояване на броя на страните на многоъгълник. Построяване на правилен петоъгълник 1 начин. Паркети от правилни многоъгълници. Правилни многоъгълници.
"Многоъгълници 8 клас" - Четириъгълници. Вътрешна зона. отстрани. Изпъкнали многоъгълници. Външна зона. Многоъгълни елементи. Сборът от ъглите на изпъкнал четириъгълник е равен на. Вертекс. близки върхове. Диагонал.
"Полигонални изгледи" - Формула: 180° *n-180° *(n-2)=360°. Защрихованата област е плосък многоъгълник. За да определите броя на страните на "правилния" n-въглен, трябва да използвате формулата. Правилни многоъгълници. Многоъгълник. Подобни многоъгълници. Връзките с общ край се наричат съседни, а точките A1 и An се наричат краища на полилинията.
"Построяване на многоъгълници" - Разнообразието от многоъгълници в света на хората. дивизияна 12 части. Разделяне на 6 равни части. Разделяне на 7 равни части. Разделяне на 8 равни части. Деление на 10 равни части. В природата, в света около нас, в ежедневието - навсякъде виждаме правилни многоъгълници. Велик и непредсказуем Питагор. Разделяне на четири равни части.