Изпълнено и това означава, че коефициентът на корелация е значителен (има връзка между

2. Изчисляване насредна грешка коефициент на корелация

Когатоr/mr³ 3, коефициентът на корелация се счита за надежден, т.е. връзката е доказана. Приr/mr3 – връзката е надеждна.

3.Метод за сравняване на контролни диаграми на медианите

Прост метод за анализ на степента на корелация е методът на медианите (методът за сравняване на графики), който е удобен за изучаване на технологичния процес, като се използват данни, получени на работното място.

Нека стойноститеxиyбъдат зададени с помощта на графики или контролни диаграми, а броят на измерванията за параметритеxиyтрябва да бъде еднакъв. Начертани са средните линии Mex, Mey. Точките над медианата се обозначават със символа "+ ", точките под медианата - със символа "- ", точките, разположени върху медианата - със символа "0".

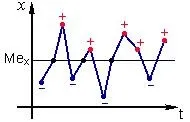
Всяка двойка стойности (x,y) съответства на двойка знаци. Двойките знаци се заменят с един код според правилата:

чифт	Код
++	+
– –	+
+ –(– +)	-
+0
– 0
0 0	+

Трябва да се изчисли следното:

- брой кодове "+ " - N(+), - брой кодове "–" - N(–), - брой кодове "0" - N(0),

След това трябва да изчислите две числаP = N(+) + N(0)/2 иM = N(–) + N(0)/2 и да намерите най-малкото от тяхmin (P, M). Според таблицата с кодови стойности за известната стойностk и дадения рисков фактор α = 1 – P (P - ниво на достоверност), трябва да намерите съответната минимална стойностнорка. Акоmin (P, M)≤ норка, тогава съществува корелация и:

приP> M-положителна (директна) корелация; когатоP 5, можем да заключим, че няма корелация, т.е. няма връзка между налягането на сгъстения въздух и процента на дефектите в процеса на леене под налягане на тънкостенни части.

Таблица 4 - Таблица с кодови стойности

к	α	к	α	к	α
0,01	0,05	0,01	0,05	0,01	0,05

4.Метод на медианата на точковата диаграма

Друг метод за анализиране на значимостта на корелационната зависимост се основава на изчертаване на вертикални и хоризонтални прави линии върху диаграмата на разсейване, съответстващи на средните стойности на променливитеxиy. Над и под хоризонталната линия, отдясно и отляво на вертикалната линия трябва да има равен брой точки. Ако общият брой точки се окаже нечетен, медианите трябва да бъдат начертани през централната точка (в примера на фигура 19 вертикалната и хоризонталната медиана ще минават през 13-та точка от класираната серия, тъй като броят на точките е 25).

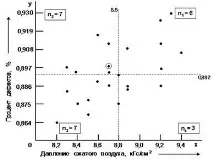
Фигура 19 - Точкова диаграма за налягането на сгъстения въздух и процент на дефектите

Във всеки от четирите квадранта, получен от разделянето на диаграмата на разсейване на вертикални и хоризонтални медиани, броят на точките се брои и се обозначава съответно като n1, n2, n3, n4. Точките, през които минава медианата, не се вземат предвид. Добавете точки поотделно в положителни (1-ви и 3-ти) и отрицателни (2-ри и 4-ти) квадранти.

Положителните и отрицателните квадранти се считат за относителниначертани върху средна точкова диаграма.

За въпросния пример:

Тъй като двете точки са на медианата, k не е равно на 25.

За да се определи наличието и степента на корелация с помощта на медианния метод, се използва и таблица с кодови стойности (Таблица 4), съответстващи на различни стойности на k при две стойности на коефициента на риск α (0,01 и 0,05).

От n(+) и n(-) се избира по-малката стойност и се сравнява със стойността на кода от Таблица 4. Прави се заключение за наличие или липса на корелация. Ако по-малкото от числата n е равно или по-малко от стойността на табличния код, тогава има корелационна зависимост. В случай, когато n(+) > n(-), тогава това показва пряка корелация, в противен случай, когато n(+) 6, може да се твърди, че в този случай няма корелация между двата параметъра, т.е. няма връзка между налягането на сгъстен въздух и процента на дефектите в процеса на леене под налягане на тънкостенни части.

Въз основа на различни методи за откриване на наличието на корелационна зависимост установяваме, че изчисленият коефициент на корелация е значим, което означава, че корелационната зависимост съществува. Въпреки това, изследването на диаграмата с помощта на метода на медианите и метода на сравняване на съответните графики показва, че не се наблюдава ясна корелация. Следователно, след извършване на един анализ или разглеждане на диаграмата на разсейване едностранчиво, е невъзможно да се каже недвусмислено за наличието на корелационна зависимост или за нейния характер (пряка, обратна и т.н.), а ако се направи такова заключение, то изисква или експериментална проверка, или допълнителни изследвания.

Понякога случайно се появява силна корелация, която изобщо не е подсилена или е подсилена твърде слабо.причинно-следствена връзка между тях. Този вид корелация се нарича фалшива корелация. Дори коефициентът на корелация да е висок, това не означава непременно причинно-следствена връзка.

---