Изследване на функция за периодичност

Секции: Математика

Цел: да се обобщят и систематизират знанията на учениците по темата "Периодичност на функциите"; формиране на умения за прилагане на свойствата на периодична функция, намиране на най-малък положителен период на функция, чертане на периодични функции; насърчаване на интереса към изучаването на математика; култивирайте наблюдение, точност.

Оборудване: компютър, мултимедиен проектор, карти със задачи, диапозитиви, часовници, декоративни маси, елементи от народните занаяти

„Математиката е това, което хората използват, за да контролират природата и себе си“A.N. Колмогоров

I. Организационен етап.

Проверка на готовността на учениците за урока. Представяне на темата и целите на урока.

II. Проверка на домашните.

Проверяваме домашните по образци, обсъждаме най-трудните точки.

III. Обобщаване и систематизиране на знанията.

1. Устна фронтална работа.

1) Формирайте дефиницията на периода на функцията 2) Назовете най-малкия положителен период на функциите y=sin(x), y=cos(x) 3). Какъв е най-малкият положителен период на функциите y=tg(x), y=ctg(x) 4) Използвайте кръга, за да докажете коректността на отношенията:

y=sin(x) = sin(x+360º) y=cos(x) = cos(x+360º) y=tg(x) = tg(x+18 0º) y=ctg(x) = ctg(x+180º)

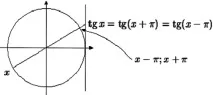
tg(x+ π n)=tgx, n € Z ctg(x+ π n)=ctgx, n € Z

sin(x+2 π n)=sinx, n € Z cos(x+2 π n)=cosx, n € Z

5) Как да начертая периодична функция?

1) Докажете следните отношения

a)sin( 740º ) = sin(2 0º )b)cos( 54º ) = cos(-1026º)c)sin(-1000º) = sin( 80º )

2. Докажете, че ъгълът от 540º е един от периодите на функцията y= cos(2x)

3. Докажете, че ъгъл от 360º еедин от периодите на функцията y=tg(x)

4. Трансформирайте тези изрази така, че ъглите, включени в тях, да не надвишават 90º по абсолютна стойност.

a)tg 375ºb)ctg 530ºc)sin 1268ºd)cos (-7363º)

5. Къде се срещнахте с думите ПЕРИОД, ПЕРИОДИЧНОСТ?

Отговори на учениците: Периодът в музиката е конструкция, в която е изложена повече или по-малко завършена музикална мисъл. Геоложкият период е част от ера и е разделен на епохи с период от 35 до 90 милиона години.

Времето на полуразпад на радиоактивно вещество. Периодична дроб. Периодичните издания са печатни издания, излизащи на строго определени дати. Периодична система на Менделеев.

6. Фигурите показват части от графиките на периодични функции. Определете периода на функцията. Определете периода на функцията.

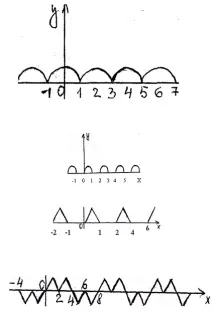
7. Къде в живота си сте се срещали с изграждането на повтарящи се елементи?

Учениците отговарят: Елементи на орнаменти, народно изкуство.

IV. Колективно решаване на проблеми.

(Решаване на проблеми на слайдове.)

Нека разгледаме един от начините за изследване на функция за периодичност.

С този метод се избягват трудностите, свързани с доказването, че един или друг период е най-малък, а също така няма нужда да се засягат въпроси за аритметични действия върху периодични функции и за периодичност на сложна функция. Разсъжденията се основават само на дефиницията на периодична функция и на следния факт: ако T е периодът на функцията, тогава nT(n? 0) е нейният период.

Задача 1. Намерете най-малкия положителен период на функцията f(x)=1+35>

Решение: Да приемем, че Т-периодът на тази функция. Тогава f(x+T)=f(x) за всички x ∈ D(f), т.е.

Нека сложим х=-0,25, получаваме

Имаме това всички периодина въпросната функция (ако съществуват) са сред целите числа. Изберете сред тези числа най-малкото положително число. Това е1. Нека проверим дали наистина е периодът1.

Тъй като = за всяко T, тогава f(x+1)=3+1=3+1=f(x), т.е. 1 - период f. Тъй като 1 е най-малкото от всички положителни числа, тогава T=1.

Задача 2. Покажете, че функцията f(x)=cos 2 (x) е периодична и намерете нейния главен период.

Задача 3. Намерете главния период на функцията

Да приемем T-периода на функцията, тогава за всекиxвръзката е вярна

sin(1.5T)+5cos(0.75T)=5

– sin(1.5Т)+5cos(0.75Т)=5

cos=1

=2πn, n ∈ Z

T=, n ∈ Z

Нека изберем от всички "подозрителни" числа за периода най-малкото положително и проверим дали това е период за f. Този номер

f(x+)=sin(1,5x+4 π )+5cos(0,75x+2 π )= sin(1,5x)+5cos(0,75x)=f(x)

Следователно е основният период на функцията f.

Задача 4. Проверете дали функцията f(x)=sin(x) е периодична

Нека T е периодът на функцията f. Тогава за всяко x

Ако x=0, тогава sinT=sin0, sinT=0 T= π n, n € Z.

Да предположим. Че за някое n числото π n е период

на разглежданата функция π n>0. Тогава sin π n+x=sinx

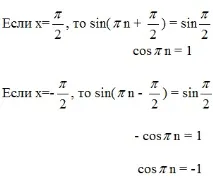
Това означава, че n трябва да бъде едновременно четно и нечетно, което е невъзможно. Следователно тази функция не е периодична.

Задача 5. Проверете дали функцията е периодична

f(x)=

Тогава нека T е периодът f

, следователно sinT=0, T= π n, n ∈ Z. Да приемем, че за някое n числото π n наистина е периодът на дадената функция. Тогава числото 2 π n също ще бъде период

Тъй като числителите са равни,тогава техните знаменатели са равни, така че

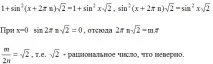
Следователно функцията f не е периодична.

Групова работа.

Задачи за 1 група.

Проверете дали функцията f е периодична и намерете главния й период (ако съществува).

Задачи за 2 група.

Проверете дали функцията f е периодична и намерете главния й период (ако съществува).

Задачи за 3 група.

В края на работата групите представят своите решения.

VI. Обобщаване на урока.

Учителят дава на учениците карти с рисунки и предлага да нарисуват част от първата рисунка в зависимост от степента, в която, както им се струва, са усвоили методите за изучаване на функцията за периодичност, а в част от втората рисунка, в съответствие с приноса им към работата в урока.

Моите умения да изследвам функции за периодичност	Моят принос към работата в урока

VII. Домашна работа

1). Проверете дали функцията f е периодична и намерете основния й период (ако съществува)

2). Функцията y=f(x) има период T=2 и f(x)=x 2 +2x за x € [-2; 0]. Намерете стойността на израза -2f(-3)-4f(3,5)

1. Mordkovich A.G.Алгебра и началото на анализа със задълбочено проучване.
2. Математика. Подготовка за изпита. Изд.Лисенко Ф.Ф., Кулабухова С.Ю.
3. Шереметьева Т.Г. , Тарасова E.A.Алгебра и началото на анализа за 10-11 клас.

---