Изследване на пасивен RC филтър (лабораторен доклад), LABA
Цел на работата: изучаване на свойствата на нискочестотните RC филтри, както и лентовите филтри, придобиване на умения за работа със специален генератор на вълни и цифров осцилоскоп.
1. Теоретично изчисляване на изрази за честотната характеристика и фазовата характеристика на филтрите
Ако сглобите делител на напрежение от двойка пасивни двуполюсници от различни типове, например от резистор и кондензатор, тогава възниква верига, която попада в понятието пасивен двуполюсник.
Очевидно изходното напрежение трябва да зависи от честотата на входното напрежение в резултат на промяната в капацитета на кондензатора.
Фазата на изходното напрежение също няма да остане непроменена, когато честотата се промени, тъй като приносът към импеданса на веригата от страна на компонента (кондензатор), който има фазово изместване между тока и напрежението, ще бъде различен за различните честоти.
Нека да изведем зависимостите, които се наричат съответно амплитудно-честотни и фазово-честотни характеристики на четириполюсника за всеки от изследваните филтри.
1.1. Едностепенен нискочестотен филтър
Този филтър (фиг. 1, а) е делител на напрежение, към който не е свързан товар. Такъв делител се нарича идеален делител на напрежение (IDN). Изходното напрежение U 2 е спадът на напрежението върху кондензатора C в този DID и следователно зависи от честотата.
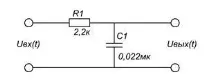
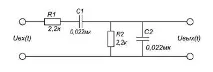
Ориз. 1. Нискочестотни филтри с една връзка (a) и две връзки (b), които се изследват,
Съгласно формулата на делителя на напрежение, съотношението на изходното към входното напрежение може да бъде изразено чрез комплексни съпротивления, подобно на резистивен делител на напрежение:
.
Продуктът RC се изразява в секунди, тогава мерната единица е 1/RC, що се отнася до ъгловата честота, ще бъде втора на минус първа степен. Нека тогава да обозначим тази стойност като w 0 и да я заместим във формула (1):
.
За да премахнем въображаемото число в знаменателя, ние умножаваме числителя и знаменателя в (2) по комплексното число, спрегнато към знаменателя:
.
От (3) може да се намери честотната характеристика като модул на този израз, а фазовата характеристика като аркутангенс на съотношението на аргументите на въображаемата и реалната част:
; .
Графично представяне на получените амплитудно-честотни и фазово-честотни характеристики е представено заедно с практически резултати на фиг.
1.2. Двусекционен нискочестотен филтър
За този филтър (фиг. 1, b) можем да използваме факта, че за изследваните синусоидални сигнали две важни свойства на последователните връзки на два или повече четириполюсници следват от правилото за умножаване на експоненциалните зависимости - получената честотна характеристика се получава чрез умножаване на честотната характеристика на отделните четириполюсници, а получената PFC се формира чрез добавяне на PFC на последователни четириполюсници:
;
.
В предишния параграф изчислихме честотната характеристика и фазовата характеристика за една връзка. Използвайки правилата (5), получаваме:
;
.
Струва си да се каже, че тъй като има само две връзки в този филтър, изразите (5) го описват доста добре, което се потвърждава от фиг. 5 и 6. В случай на по-голям брой секции, делителите на напрежението са още по-несъвършени, тъй като техните изходи се шунтират от изходите на следващите секции, но използвайки примера на двустепенен филтър, по този начин показахме прост начин за оценка на печалбата.
Подобно на първоначалните изчисления, този филтър (фиг. 1, c) може да се разглежда като делител на напрежение със сложни съпротивления, представени от последователни и паралелнисвързване на резистор и кондензатор. Ето защо:
Както преди, обозначаваме продукта със стойността 1/ RC като w 0 и, замествайки, получаваме:
.
От (7) може да се намери честотната характеристика като модул на този израз, а фазовата характеристика като аркутангенс на съотношението на аргументите на въображаемата и реалната част:
; .
2.1. Характеристики на едностъпален нискочестотен филтър
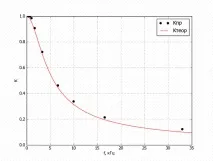
Ориз. 2. Теоретична (1) и експериментално получена (2) честотна характеристика
едносекционен RC нискочестотен филтър
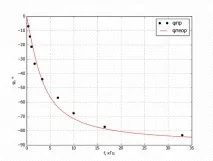
Ориз. 3. Теоретичен ( 1) и експериментално получен ( 2) PFC
едносекционен RC нискочестотен филтър
2.2. Характеристики на двусекционен нискочестотен филтър
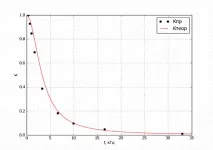
Ориз. 4. Теоретична (1) и експериментално получена (2) честотна характеристика
двусекционен RC нискочестотен филтър
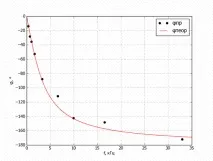
Ориз. 5. Теоретичен (1) и експериментално получен (2) PFC
двусекционен RC нискочестотен филтър
2.3. Характеристики на филтъра за вино
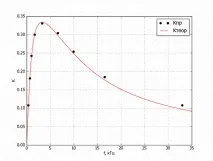
Ориз. 6 Теоретично ( 1) и експериментално получено ( 2) А
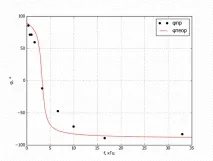
Ориз. 7. Теоретичен (1) и експериментално получен (2) PFC
1. Нискочестотният филтър пропуска само нискочестотни сигнали (фиг. 2 и 4). Както се вижда от сравнението на получените графики, стръмността на амплитудно-честотната характеристика може да се увеличи чрез използване на каскадно свързване на едносекционни филтри, в нашия случай - два. В този случай граничната честота остава същата и потискането на високите честоти е по-добро. В този случай фазовото отместване се увеличава до два пъти поради приноса на втория капацитет (фиг. 3 и 5).
2. Комбинациите от нискочестотни и високочестотни филтри ви позволяват да създавате лентови филтри, с помощта на които самоопределен честотен диапазон. Тази възможност е демонстрирана с помощта на филтъра Wien (фиг. 6). Максималното усилване, за разлика от LPF, е 1/3.
3. Простите филтри се поддават добре на теоретично описание, както може да се види от получените експериментални характеристики и сравнение с математически изчисления. Неравномерността на грешките е свързана с нелинейните закони на честотното разпределение и измервателната скала.