Изучаване на законите на топлинното излъчване

Целта на работата: да се запознаят с оптичния метод за измерване на температурата, да проверят закона на Кирхоф, да определят константата на Стефан-Болцман; за изследване на зависимостта на топлинното излъчване (енергийна светимост или интегрална излъчвателна способност) на абсолютно черно тяло от температурата.

Уреди и оборудване: оптичен пирометър, волтметър, амперметър, реостат, електрическа лампа; EP електрическа пещ, радиационен приемник (TC термоколона), блок за управление и индикация (BUI).

При топлинно движение атомите и молекулите могат да преминават в състояния с по-висока енергия (възбудени състояния), а при обратния преход се излъчват електромагнитни вълни. Следователно такова излъчване се нарича топлинно. Топлинното излъчване се осъществява при всяка температура T0 K, но при ниски температури на практика се излъчват само дълги (инфрачервени) електромагнитни вълни. Спектърът на топлинното излъчване е непрекъснат.

Важна характеристика на топлинното излъчване е, че то може да бъде в равновесие. По това се отличава от всички останали видове радиация. Ако нагрято тяло се постави в кухина с идеално отразяващи стени, тогава с течение на времето в резултат на непрекъснат обмен на енергия между тялото и радиацията ще настъпи равновесие, т.е. тялото ще абсорбира толкова енергия за единица време, колкото излъчва.

Нека се запознаем с основните характеристики на топлинното излъчване. Енергийната осветеност или излъчвателна способност е енергията, излъчвана от единица повърхност на тяло за единица време при температура T:

, (4.1)

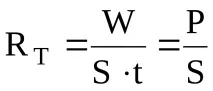
където W е енергията, излъчена за времето t от цялата повърхност на тялото;

– мощност на излъчената енергия. Тази енергия се пренася от електромагнитни вълни с всякаква дължина.

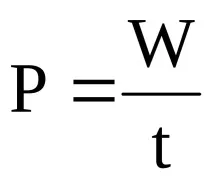
Разпределението на енергията в спектъра на излъчване се характеризира сспектрална плътност на блясъка. Измерва се чрез енергията dRT, излъчвана в тесен диапазон от дължини на вълните d за единица време на единица площ:

.

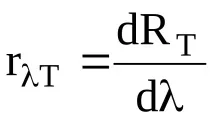
Има очевидна връзка между излъчвателната способност и спектралната плътност на излъчвателната способност:

.

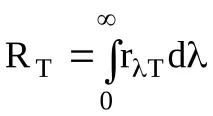
Полученият експериментално емисионен спектър при Т=const е показан на фиг. 4.1.

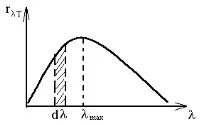
Енергията, излъчена в интервала d, е равна на площта на защрихованата лента, а общата излъчена енергия (лъчение) е равна на площта под кривата

. От графиката може да се види, че енергията, излъчвана от различните дължини на вълните, варира значително. В допълнение, графиката има ясно изразен максимум на спектралната плътност на блясъка.

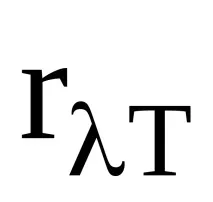
Абсорбционният капацитет aT е съотношението на радиационния поток (мощност) dWabs., абсорбиран в тесен спектрален диапазон от дължини на вълните от  до +d от единица повърхностна площ на тялото, към радиационния поток dW, падащ върху единица повърхност в същия спектрален интервал:

.

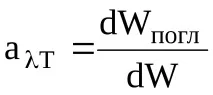
Капацитетът на поглъщане на тялото зависи от дължината на вълната  и температурата на тялото, както и от природата на тялото.

По дефиниция aT не може да бъде по-голямо от едно. Тяло, което поглъща цялата енергия, която пада върху него, се нарича абсолютно черно. За него aT=1. Тяло, което поглъща еднакво във всички интервали на дължина на вълната (aT=const1), се нарича абсолютно сиво тяло. Зависимостта на aT от  за тези две тела е показана на фиг. 4.2.

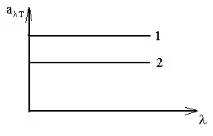
Линия 1 се отнася за aT на напълно черно тяло, линия 2 - за aT на напълно сиво тяло.

Връзката между спектралната плътност на излъчването и абсорбцията се установява от закона на Кирхоф:

, (4.2)

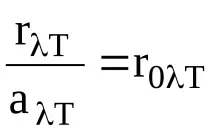
тези. съотношението на спектралната плътност на излъчвателната способност на тялото към неговата абсорбционна способност е еднакво зана всички тела, не зависи от тяхната природа и е равна на спектралната плътност на излъчвателната способност на напълно черно тяло

при дадена температура и дължина на вълната.

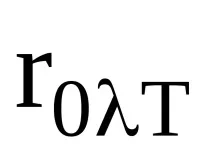
Така законът на Кирхоф постави дефиницията на функцията

в центъра на вниманието на теорията на топлинното излъчване. Но исторически, в началото теоретично и експериментално са установени следните закони, които определят някои от основните характеристики на функцията eT:

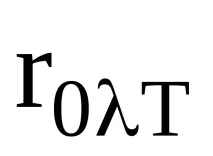
Закон на Стефан-Болцман. Коефициентът на излъчване на черно тяло (ABC) R0Т е пропорционален на четвъртата степен на абсолютната му температура, т.е.

, (4.3)

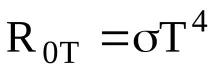
където =5,6710 -8 W/m 2 K 4 е константата на Стефан-Болцман.

Законът за изместване на Виен. Дължината на вълната max, която отчита максималната спектрална плътност на енергийната яркост на напълно черно тяло, е обратно пропорционална на неговата абсолютна температура, т.е. с повишаване на температурата максималната енергийна плътност на светимост се измества към къси вълни (фиг. 3).

,

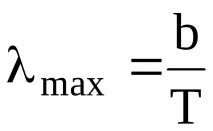
където b=2,8910 -3 mK е константата на Wien.

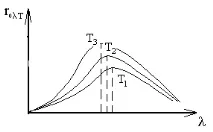
Вторият закон на Виена. Максималната стойност на спектралната плътност на енергийната светимост е правопропорционална на петата степен на абсолютната температура, т.е.

където c \u003d 1,310 -5 W / m 3 K 5 е константата на втория закон на Wien.

Опитът за теоретично извеждане на зависимостта r0T принадлежи на английските учени Д. Рейли и Д. Джийнс, които приложиха методите на статичната физика за обяснение на топлинното излъчване, използвайки класическия закон за равномерно разпределение на енергията по степени на свобода.

Формулата на Rayleigh-Jeans за излъчване на черно тяло е следната:

, (4.4)

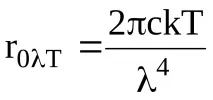
където k е константата на Болцман.

Опитът показва, че израз (4.4) е в съответствие с експерименталните данни само вобласти с достатъчно дълги дължини на вълните. В областта на малките дължини на вълните формулата на Rayleigh-Jeans рязко се различава от експеримента (фиг. 4.4).

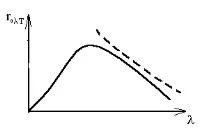
Освен това формулата на Rayleigh-Jeans води до абсурден резултат и за общата излъчвателна способност. защото

,

тогава общата излъчвателна способност на черното тяло трябва да бъде безкрайно голяма. Този резултат се нарича "ултравиолетова катастрофа". Така в рамките на класическата физика не беше възможно да се обяснят законите за разпределение на енергията в спектъра на абсолютно черно тяло.

Изход от тази ситуация е намерен през 1900 г. от М. Планк, който изказва хипотезата, че светлината се излъчва и поглъща на отделни порции или кванти. Стойността на квантовата енергия се изразява с формулата

,

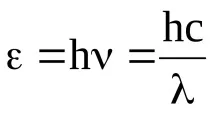
където h=6,6210 -34 Js – константа на Планк;  - честота на излъчване; с=310 8 m/s е скоростта на светлината във вакуум.

От тази формула се вижда, че с намаляване на дължината на вълната  стойността на квантовата енергия нараства. Спектралната плътност на излъчването r0Т се определя не само от стойността на енергията на съответните фотони, но и от техния брой. Планк извежда формула, която дава възможност да се определи стойността на r0Т

или,

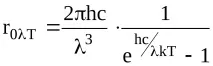
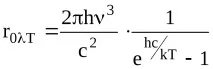
където c е скоростта на светлината във вакуум; k е константата на Болцман; e е основата на натуралния логаритъм.

От формулата на Планк, чрез математически трансформации, могат да се получат всички закони на излъчването на черното тяло.

Отличното съответствие между формулата на Планк и експерименталните резултати потвърждава хипотезата на Планк за квантовата природа на светлината.

ЗАДАЧА 1. Проверка на закона на Кирхоф.

В тази лабораторна работа трябва да проверите закона на Кирхоф. От (4.2) следва, че за сиво тяло

---