Как да изчислим минималните общи разходи за съхраняване на инвентара и
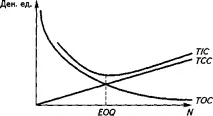
Фиг. 10.1. Модел на партида за оптимална поръчка
Графиката показва основните предпоставки на модела: част от разходите се увеличават с нарастването на запасите, а част намаляват. Оптималният размер на поръчката е този, който минимизира общите разходи. Близо до оптималната точка кривата на разходите намалява постепенно, леко. Това предполага, че малката флуктуация в размера на партидата на поръчката не влияе фундаментално на разходите. Аналитично оптималният размер на поръчката (EOQ точка) се определя чрез диференциране на уравнение (10.6) по отношение на Q (поръчано количество). Приравняването на производната на нула ви позволява да намерите минималната цена: dTIC _ cf AS dQ 2 Q2
' оттук EOQ = y]2FS / СР. (10.7) Този израз се нарича формула на Уилсън. Пример. Нека една организация използва годишно 3500 m3 дървесина (средно 10 m3 на ден). Цената на единица запас (1 m3) е 2000 рубли. Фиксираните разходи за организиране на една поръчка са 15 000 рубли. Разходите за съхранение се състоят от следните стойности: годишно складова и счетоводна работа - 72 000 рубли. годишно амортизация на складови съоръжения - 48 000 рубли. на година комунални услуги - 24 000 рубли. на година; застраховка - 5% от средната цена на единица материал; марж и намаление - 6% от цената на единица материал; цена на капитала - 10% от цената на единица материал. За да определите цената на съхранението, трябва да изчислите: застрахователни разходи: 3500 • 2000 • 0,05 = 350 000 рубли брак и намаление: 3500 • 2000 • 0,06 = 420 000 рубли; Така че разходите за съхранение са: 180 000 + 72 000 + 48 000 + 24 000 + 350 000 + 420 000 + 700 000 = =1 794 000 рубли, и нивото на разходите за съхранение ще бъде 1 794 000/7 000 000-100% = = 26% от стойността на инвентара. Сега имаме всички данни за изчисляване на оптималната партида за поръчка: EOQ = V2-15 000-3500/0,3-2000 = 420 m3. A t средна дневна консумация на строителни материали 10 m3 (3500/360) от внесената партида е достатъчна за около месец и половина (420/10). Средният запас е равен на половината от EOQ, т.е. 210 m3 или в стойностно изражение: 210 • 2000 = 420 000 рубли. Цената на всяка покупка при постоянни цени ще бъде: 420 • 2000 = 840 000 хиляди рубли. Въпреки това, като се вземе предвид инфлацията, всяка нова покупка ще струва повече. Например, при инфлация, равна на 1% на месец, разходите за закупуване на партида по номинална стойност могат да бъдат 840 000 (1 + 0,1) = 848 000 хиляди рубли. или 840 000 (1 + 01) 2 = = 857 900 хиляди рубли Разликата се дължи на специфична ситуация: при месечна инфлация от 1% строителните материали ще се повишат в цените веднъж или два пъти за месец и половина.