Класификация на състоянията на веригатаМаркова
Нека въведем класификация на състоянията на веригата на Марков. Наборът от всички състояния може да бъде разделен на неприпокриващи се подмножества или класове:невръщащи се и
ергодични. Техните свойства се определят както следва. След като процесът напусне клас от първия тип, той никога не се връща към него. Ако процесът е в класа на състоянията от втори тип, тогава той никога не го напуска. Ще обозначим необратимото множество сT,и ергодичното множество с Ť.Освен това,TuŤ=S,T∩T = 0 .Ако едно ергодично множество съдържа само едно състояние, тогава това състояние се нарича абсорбиращо. За такова състояние S елементът на преходната матрицарiiтрябва да бъде равен на 1, следователно всички останали елементи на съответния ред са равни на 0. Верига, чиито алергични състояния са абсорбиращи, се нарича абсорбираща верига.
За верига на Марков сNсъстояния, в които има както необратими, така и ергодични множества, структурата на матрицата на вероятността за преход (възможно след преномериране на състоянията) има каноничната форма
къдетоs -е броят на състоянията в набора без връщане;
n - s -брой състояния в ергодичното множество.
МатрицатаWс измерение(n-s)x(n-s)определя динамиката на ергодичните състояния. Тъй като е невъзможно да се напусне множеството Ť, матрицата Ø с размерност (n-s)x s се състои от нули.
МатрицаQна измерениеsxsопределя поведението на процеса до излизането от множеството невръщащи се състояния.
МатрицатаRс измерениеs x(n — s)определя вероятностите за преход от набора от състояния без връщане към вергодичния набор.
При повишаване на матрицатаPна степен, блоковете, посочени в (3.9), се умножават и произволностепента на каноничната матрица има формата
Разгледайте структурата на матрицатаR(k).Изчислявайки последователно степените на матрицатаP, като вземем предвид (3.9), получаваме:
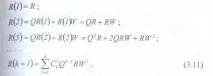
къдетоСk i -биномни коефициенти. В съответствие с горното,iтият ред на матрицатаR(k)съдържа вероятностите за преход на системата към всички състояния на ергодичното множество Ť вkстъпки, когато се стартира от състоянието Si ∈ T.
Ако веригата на Марков е поглъщаща, тогаваW = Iе идентична матрица с измерениеn - s,и всички нейни степени също са идентична матрица със същото измерение.
Отбелязваме още два специални вида матрици на вероятностите за преход.
МатрицаPсе нарича редуцируема, ако има формата
където A иB -са квадратни, Ø- нулеви матрици.
Верига на Марков, дефинирана от матрица от вида (3.12), всъщност се разделя на две независими вериги на Марков, дефинирани съответно от матрицитеAиB.
МатрицаPсе нарича периодична, ако има формата
където нулевите матрици са квадратни. Има и два набора от състояния и на всяка стъпка процесът преминава от един набор от състояния в друг. Това е точно структурата на преходната матрица в горния пример, ако разгледаме преходната матрица вътре в набора от невръщащи се състояния.
| следваща лекция ==> | ||
| Определение на веригата на Марков | Оценка на продължителността на престоя на процеса в множеството невръщащи се състояния |
Не намерихте това, което търсихте? Google да ви помогне!