Клен Бележки по - теоретична физика
Хокейно предизвикателство - 2
Нека продължим да решаваме "хокейния проблем". В последния пост разгледахме вариант на проблема с изкуственото поддържане на постоянна скорост на въртене на пръстена. Сега нека да преминем към опцията, когато поради триене се забавя не само транслационното движение, но и въртенето.
Спомнете си, че динамиката на пръстена се описва от уравненията
където $$v$$ е скоростта на транслационното движение, $$u=\omega R$$ е скоростта на въртеливото движение на пръстена.
Системата от уравнения (1) е симетрична по отношение на замяната на $$u$$ с $$v$$. Ако в началния момент $$u=v$$, то от съображения за симетрия тази връзка ще се запази между скоростите до спиране. Другият случай, който ще разгледаме, е $$u>v$$. Обратният случай $$u v
За съжаление интегралите в система (1) се свеждат до елиптични, което не оставя надежда за аналитично решаване на системата. Остава численото решение.
Директен опит за решаване на уравнението в Maple се проваля. Определените интеграли са заменени с купчина елиптични интеграли, които няма смисъл да представяме тук. При изчертаване виждаме съобщение за грешка
За да опростим изразите, ние налагаме ограничението $$u(t)\ge v(t)\ge 0$$ на всеки от интегралите.
Ограниченията премахват съобщението за грешка. Maple мисли дълго време, но показва празна графика. За да разберем причината, извеждаме решението на уравнението в даден момент.
$$[t=1.,\\u(t)=10.9976102709142-2.84005015829721 10^,\\v(t)=1.04887416587408+2.92542849266058 10^]$$
Натрупването на грешка при закръгляване води до появата на ненулева имагинерна част в желаните функции, поради което графиката е празна. За да избегнем появата на въображаемата част, ние вземаме реалната част от десните части на уравненията в ясна форма:
Най-накрая, Maple, дълго мислене, всичкосъщо чертае графика.
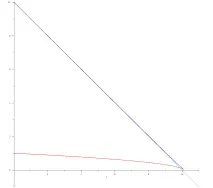
В същото време виждаме предупреждение за точката на спиране на изчислението, което очевидно съвпада с края на движението:
Предупреждение, не мога да оценя решението по-вдясно от 10.155665, вероятно сингулярност
За численото решение сме избрали начална транслационна скорост 1 и скорост на въртене 10. Без въртене пръстенът се движи на разстояние 0,5 за 1 единица време. Наличието на въртене доведе до факта, че транслационното движение се поддържа повече от 10 единици време.
Линеаризирано решение за u >> v
Графиката на $$u(t)$$ - синята линия - почти съвпада с правата линия. Графиката $$v(t)$$ - червената линия - прилича на парабола. Такова поведение се предсказва от линеаризираното решение в ограничението $$u\gg v$$. Пренебрегвайки $$v$$ в първото уравнение на системата (1) и разширявайки второто по степени на $$p=v/u$$, получаваме
Решението на тази система са функциите $$u(t)=u_0-t$$, $$v(t)=v_0\sqrt$$. Техните графики са показани със сиви линии.
Както виждаме от численото решение и графиката, апроксимацията правилно описва природата на движението, докато $$u$$ и $$v$$ станат сравними. Ето графика за случая, когато едната скорост е два пъти по-голяма от другата:
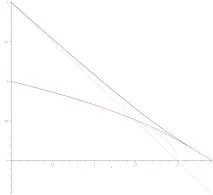
Тук разликата от линеаризираното решение се забелязва почти веднага.
Начин за спиране: Линеаризирано приближение
Пътят, изминат от пръстена, се дава от площта на криволинейния трапец под червената линия. В линеаризираното приближение криволинейният трапец е ограничен от парабола и, както е лесно да се види, има площ $$l=2u_0v_0/3$$. Ако пръстенът не се въртеше, той щеше да измине разстоянието $$l_0=v_0^2/2$$. По този начин, за да увеличите проходимия път с 5 пъти, трябва да завъртите пръстена с ъглова скорост
Спомнете си това, за да преминетепо пръстена на същия път, с постоянно въртене, скоростта му трябва да бъде три пъти по-малка: $$\omega_0=(5/4)\,$$.
Начин за спиране: Числено решение
Сега нека изчислим проходимия път от оригиналните уравнения, без линеаризация.
По някаква причина Maple не намери точка на спиране („сингулярност“) за първоначалната стойност от 15/4 и неправилно продължи решението. Приблизителната позиция на тази точка се намира чрез селекция.
Изчисляването на последния резултат на Maple отне повече от 10 минути. Както можете да видите, за първоначалната стойност от 15/4, грешката на линеаризираното приближение е 2%.
Решихме „хокейната задача“ в оригиналната опростена формулировка и без опростявания в линеаризираното приближение. Използвайки системата за компютърна алгебра на Maple, ние се уверихме, че за условието на този проблем линеаризираното приближение дава грешка от няколко процента.
хокейно предизвикателство
Тънък пръстен лежи върху грапава хоризонтална повърхност. След натискане към центъра на пръстена, той се премества на определено разстояние. Когато този пръстен се завъртя до определена ъглова скорост (поддържана постоянна за цялото време на движение), тогава при същата начална скорост пръстенът измина $$k$$ пъти по-голямо разстояние. Как беше рекламиран този пръстен? (опитайте се да намерите нелинейна корекция в отговора). (V.S. Bulygin)
Използвайки този проблем като пример, искам да покажа как да използвам компютърни алгебрични системи, по-специално Maple.
При условие на поддържане на постоянна ъглова скорост на въртене изглежда изкуствено. Това изискване опростява проблема, така че да може да бъде решен на олимпиадата. В тази публикация ще разгледаме такава формулировка, а в следващата - загубата чрез триене не само на транслационна скорост, но и на ротационна.
Физическата страна на проблема
Решението на задачата е анализиранона Елементите (там го наричаха „хокеен проблем“). Физическата част на решението не изисква излизане отвъд училищните знания, няма да се спираме на нея. Нека разгледаме по-отблизо математиката. Нека започнем със системата от уравнения, извлечена от връзката по-горе:
Тук $$v$$ е скоростта на транслационното движение, $$u=\omega R$$ е скоростта на въртеливото движение на пръстена.
Уравненията са такива, че можем да се отървем от незначителния фактор $$\mu g$$ чрез подходящ избор на единица време, така че ще го пропуснем в дискусията по-долу.
Ограничен режим
Ако приемем, че $$u=const$$, уравнението за $$v$$ има прост граничен режим, когато $$v\to 0$$. След това, като разширим подинтегралната функция в поредица от $$v$$ до втория ред на малкост и интегрирайки, виждаме, че намаляването на скоростта е пропорционално на самата скорост. При ниски скорости пръстенът спира експоненциално, сякаш триенето не е сухо, а течно.
Случай на постоянна скорост на въртене
По условие ъгловата скорост на въртене се поддържа постоянна, а линейната скорост пада до 0. Логично е да приемем, че имаме работа с режим $$0$$. Нека $$p=v/u$$. Тогава
Пръстенът изминава известно разстояние, преди да спре
Заместете $$dt$$ от (2) в (3):
Когато няма въртене, пръстенът се движи равномерно и изминава разстоянието $$l_0=v_0^2/2$$. Въртящият се пръстен изминава $$k=5$$ пъти разстоянието $$l$$:
Заместете $$l$$ в (4) и разделете на $$p_0^2$$:
Това уравнение ни дава връзката между началната скорост на въртене на пръстена $$\omega_0=v_0/(p_0R)$$ и нарастването на изминатото разстояние до спирането $$k$$.
Числено решение в Maple
Вътрешният интеграл се изразява чрез елиптични интеграли. Maple обаче не знае нищо за знака $$p$$ исъздава тромав израз, съдържащ фрагменти като $$\sqrt>$$, csgn(p-1). Нека предложим очевидно ограничение на $$p$$:
След това е лесно да се намери отговорът $$p_0$$ с необходимата точност:
В началния момент скоростите на транслация и въртене бяха свързани с отношението $$v_0\approx0,\!78\,\omega_0R$$.
Приблизителен отговор може да се получи не само числено, но и чрез разлагането на вътрешния интеграл в редица
Нека изчислим лявата страна на (5) за $$p_0=0,\!78$$, като последователно прецизираме разширението на вътрешния интеграл:
Въпреки че първоначалната стойност на параметъра $$p_0=v_0/u_0=0,\!78$$ не може да се нарече малка, линеаризацията по този параметър дава грешка по-малка от 3%. За линейно приближение отговорът би бил $$p_0=4/k=0,\!8\,$$. И като се вземе предвид кубичната корекция вече дава грешка под процент.