KNOW INTUIT, Лекция, Алгоритми за симетрично криптиране

мрежа на Feistel

Блоковият алгоритъм преобразува n-битов блок от обикновен текст в n-битов блок от шифрован текст. Броят на блоковете с дължина n е 2 n. За да бъде трансформацията обратима, всеки от тези блокове трябва да бъде трансформиран в свой собствен уникален блок за шифрован текст. С малка дължина на блока такова заместване не прикрива статистическите характеристики на некриптирания текст. Ако блокът е с дължина 64 бита, тогава той вече добре скрива статистическите характеристики на изходния текст. Но в този случай трансформацията на текста не може да бъде произволна поради факта, че самата трансформация ще бъде ключова, което изключва ефективни както софтуерни, така и хардуерни реализации.

Мрежите на Feistel са най-широко използваните, тъй като, от една страна, те отговарят на всички изисквания за симетрични алгоритми за криптиране, а от друга страна, те са доста прости и компактни.

Мрежата на Feistel има следната структура. Входният блок е разделен на няколко подблока с еднаква дължина, наречени разклонения. Ако блокът е с дължина 64 бита, се използват две разклонения от по 32 бита. Всеки клон се обработва независимо от другия, след което се извършва циклично изместване на всички клонове наляво. Тази трансформация се извършва в продължение на няколко цикъла или кръга. В случай на два клона, всеки кръг има структурата, показана на фигурата:

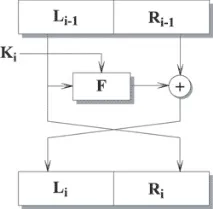
Функцията F се нарича генератор. Всеки кръг се състои от оценяване на функцията F на един клон и побитово XOR на резултата от F с другия клон. След това клоните сменят местата си. Смята се, че оптималният брой кръгове е от 8 до 32. Важно е, че увеличаването на броя на кръговете значително увеличавакриптографска сила на алгоритъма. Може би тази функция е повлияла на такова активно разпространение на мрежата Feistel, тъй като за по-голяма криптографска сила е достатъчно просто да увеличите броя на кръговете, без да променяте самия алгоритъм. Напоследък броят на кръговете не е фиксиран, а се посочват само допустимите граници.

Мрежата на Feistel е обратима, дори ако функцията F не е, тъй като дешифрирането не изисква изчисляване на F -1. За декриптиране се използва същият алгоритъм, но шифрованият текст се използва като вход, а ключовете се използват в обратен ред.

Днес все повече се използват различни варианти на мрежата Feistel за 128-битов блок с четири разклонения. Увеличаването на броя на клоновете, а не на размера на всеки клон, се дължи на факта, че процесорите с 32-битови думи все още са най-популярни, следователно е по-ефективно да се работи с 32-битови думи, отколкото с 64-битови.

Основната характеристика на алгоритъма, базиран на мрежата на Фейстел, е функцията F . Различни опции също се прилагат за първоначалните и крайните трансформации. Такива трансформации, наречени избелване, се извършват, за да се извърши първоначално рандомизиране на входния текст.

Криптоанализ

Процесът, чрез който се прави опит да се открие X, K или и двете, се нарича криптоанализ. Една от възможните атаки срещу алгоритъма за криптиране е brute force атака, т.е. просто изброяване на всички възможни ключове. Ако наборът от ключове е достатъчно голям, тогава избирането на ключ е нереалистично. При дължина на ключа от n бита, броят на възможните ключове е 2 n. Следователно, колкото по-дълъг е ключът, толкова по-устойчив се счита алгоритъмът за фронтална атака.

Има различни видовеатаки, базирани на факта, че противникът знае определен брой двойки некриптирано съобщение - криптирано съобщение. Когато анализира шифрован текст, противникът често използва статистически методи за анализ на текст. В същото време той може да има обща представа за вида на текста, например английски или български текст, изпълним файл на конкретна ОС, изходен текст на определен език за програмиране и др. В много случаи криптоаналитикът има доста информация за изходния текст. Криптоаналитик може да е в състояние да прихване едно или повече некриптирани съобщения заедно с тяхната криптирана форма. Или криптоаналитикът може да знае основния формат или основните характеристики на съобщението. За една криптографска схема се казва, че е абсолютно защитена, ако криптираното съобщение не съдържа никаква информация за оригиналното съобщение. Казва се, че една криптографска схема е изчислително сигурна, ако:

Цената за дешифриране на съобщение е по-висока от цената на самото съобщение.
Времето, необходимо за дешифриране на съобщението, е по-дълго от живота на съобщението.

Диференциален и линеен криптоанализ

Нека разгледаме в общи линии основния подход, използван в диференциалния и линейния криптоанализ. И в двата случая се приема, че са известни достатъчно голям брой двойки (чист текст, шифрован текст).

Концепцията за диференциален криптоанализ е въведена от Ели Бихам и Ади Шамир през 1990 г. Крайната цел на диференциалния криптоанализ е да се използват свойствата на алгоритъма, главно свойствата на S-кутията, за определяне на подключа на кръга. Конкретният метод на диференциален криптоанализ зависи от въпросния алгоритъм за криптиране.

Ако алгоритъмът е базиран на мрежаФейстел, тогава можем да приемем, че блокът m се състои от две половини - m0 и m1 . Диференциалният криптоанализ разглежда разликите, които възникват във всяка половина, когато са криптирани. (За алгоритъма DES "разликите" се определят с помощта на операцията XOR, за други алгоритми е възможен различен метод). Избира се двойка некриптирани текстове с фиксирана разлика. След това разликите, получени след криптиране с един кръг на алгоритъма, се анализират и се определят вероятностите на различните ключове. Ако за много двойки входни стойности, които имат еднаква разлика X, когато се използва един и същ подключ, разликите на съответните изходни стойности се окажат еднакви (Y), тогава можем да кажем, че X предполага Y с определена вероятност. Ако тази вероятност е близка до единица, тогава можем да предположим, че кръглият подключ е намерен с тази вероятност. Тъй като кръговете на алгоритъма са независими, вероятностите за намиране на подключа на всеки кръг трябва да се умножат. Както си спомняме, предполага се, че резултатът от криптирането на дадена двойка е известен. Резултатите от диференциалния криптоанализ се използват както при разработването на специфични S-кутии, така и при определяне на оптималния брой кръгове.

Друг начин за криптоанализ е линейният криптоанализ, който използва линейни приближения на трансформациите, извършени от алгоритъма за криптиране. Този метод ви позволява да намерите ключа, като имате достатъчно голям брой двойки (обикновен текст, шифрован текст). Помислете за основните принципи, на които се основава линейният криптоанализ. Обозначете