KNOW INTUIT, Лекция, Интеграция

Интеграция

По-горе разгледахме основния проблем на диференциалното смятане - намирането на производната за всяка дадена диференцируема функция. Обратният на този проблем е основният проблем на интегралното смятане - проблемът за възстановяване на функция от дадената й производна. Такива задачи се наричат ​​обратни една на друга или взаимно обратни.

Функция F(x) се нарича антипроизводна (или примитивна) за някаква функция f(x) на даден интервал, ако равенството F'(x)=f(x) е вярно във всяка точка от този интервал, или еквивалентно, в диференциална форма: dF(x)=f(x)dx.

Проблемът с намирането на първоизводната за функцията f(x) се решава нееднозначно: ако F(x) е първоизводната на f(x) , то функцията F(x)+C , C - const също е нейната първоизводна. Наистина, това следва от конструктивните правила за намиране на производната сума и константата, според които (F(x)+C)' = F'(x) = f (x) .

Теорема. Ако F(x) е първоизводната f(x) на интервала X, тогава всяка друга първоизводна на този интервал може да бъде записана като F(x)+C, тоест тя се различава от F(x) с постоянен член; техните графики са успоредни.

Неопределеният интеграл на функция f(x) е колекцията от всички първоизводни f(x) . Неопределеният интеграл се означава като .

Тук функцията f(x) се нарича интегранд; променлива x - интегрална променлива (интегрална променлива), f(x),dx - интегрална функция, f(x) - интегрална функция.

Използвайки знанието за производната на функцията F(x), можете да намерите редица прости интеграли.

Пример. Според таблицата с производни могат да се възстановят интеграли от следния вид:

.

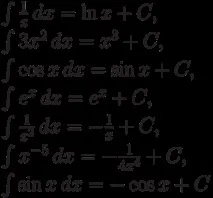
Проблемът за намиране на неопределения интеграл ( първоизводна) се нарича интегриране на функцията f(x) . Интегрирането е обратна операция на диференцирането и резултатът от интегрирането може да бъде проверен чрез диференциране. Резултатът от диференцирането може да се провери и чрез интегриране.

Всички антипроизводни от предишния пример лесно се проверяват за коректност с помощта на таблицата с производни. Но ако производната не е таблична, резултатът може да се провери и чрез диференциране.

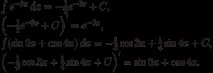
Представяме основните свойства на неопределения интеграл.

1. Производната на неопределения интеграл е равна на интегралната функция: .
2. Диференциалът на неопределения интеграл е равен на интегранта: .
3. Неопределеният интеграл на производната на функция се различава от самата функция само с постоянна стойност: .
4. Постоянният фактор може да бъде изваден от знака на неопределения интеграл. .
5. Неопределеният интеграл от сумата на функция е равен на сумата от интегралите на тези функции: .
6. Неопределеният интеграл на разликата на функция е равен на разликата на интегралите на тези функции: .

Използвайки таблицата с производни, можете да напишете (и трябва да запомните) следната таблица с неопределени интеграли:

1. .
2. .
3. .
4. .
5. .
6. .
7. .
8. .
9. .
10. .

Използвайки свойствата на неопределените интеграли и таблицата на основните интеграли, някои функции могат да бъдат интегрирани.

Пример. Лесно се проверява валидността на следните равенства:

1. .
2. .
3. .

В общия случай няма правила за интегриране на продукт, конкретна, сложна, обратна функция. Има само отделни методи за интегриране на определени класове функции.

Помислете за най-честоизползваната техника (метод) на интегриране е методът за замяна на променлива, чиято същност е следната.

Ако интегралът е труден за изчисляване, тогава вместо този интеграл можете да изчислите равен на него интеграл (вижте свойствата на интеграла), който се получава чрез заместване на променливата x в първоначалния интеграл по формулата. При добър избор на тази замяна последният интеграл може да се изчисли лесно или дори да бъде табличен. След като този интеграл се изчисли с помощта на заместването, е необходимо да се върнете към "старата" променлива x, т.е. да замените обратното заместване.

Пример. . Замяна x-1=t , откъдето лесно можем да намерим обратната замяна x=t+1 , (т.е. функцията , както и изразът за dx, необходими за заместване във формулата чрез новата променлива t или . В резултат на замяната можем да запишем следната верига от равенства: .

Друг често използван метод за изчисляване на интеграли е методът на интегриране по части. Същността на този метод е следната.

Нека функциите u=f(x) , v=g(x) са непрекъснати заедно с техните производни от първи ред на някакъв интервал. След това има формула, наречена формула за интегриране по части: , или . Тази формула ви позволява да намалите изчисляването на някой по-сложен интеграл до изчисляването на по-прост интеграл от формата , който дори може да бъде табличен или да бъде намален до такъв.

Основните препоръки за интегриране могат да бъдат сведени до следните основни правила.

Като функция u трябва да се избере една от функциите f, g, която има по-проста производна, а за dv да се вземе диференциалът на тази функция от тях, който лесно ще се интегрира.

Пример. Нека изчислим интеграла. Нека x=u , тогава , du=dx , , . Вторият избор на функция само ще усложни изчислението, намалявайки изчисления интеграл до още повечекомплекс: ако e x =u , , , , тогава .

За да се получи крайният резултат, често трябва последователно да се прилага формулата за интегриране по части няколко пъти.

Пример.

.

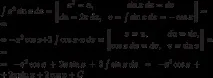
Тук двойните вертикални линии съдържат всички изчисления, които са подготвителни за прилагането на формулата за интегриране по части.

---