KNOW INTUIT, Лекция, Основни понятия от теорията на абстрактните автомати

"Теория на автоматите" е един от важните компоненти на федералния държавен стандарт в областта на "Компютърни науки и компютърна техника".

Теорията на автоматите има широк спектър от приложения:

• Проектиране на системи за логическо управление;
• Текстообработка и изграждане на компилатор;
• Специфициране и проверка на системи от взаимодействащи процеси;
• Езици за описание на документи и обектно-ориентирани програми;
• Оптимизация на логически програми и др.

Това може да се съди по презентациите на семинара "Софтуер 2000 ..." на учени и специалисти.

Дъг Рос: "...80 или дори 90% от компютърните науки (Computer Science) в бъдеще ще се основават на теорията на крайните автомати ..."

Herver Gallaire: „Познавам хора от Boeing, които работят върху системи за стабилизиране на самолети, използвайки чиста теория на автоматите. Трудно е да си представим какво са направили с тази теория.“

Brian Randell: "Голяма част от теорията на автоматите е била успешно използвана в системни програми и текстови филтри в UNIX. Това позволява на много хора да работят на високо ниво и да разработват много ефективни програми."

1.1. Основни понятия и определения.

Най-простият преобразувател на информация (фиг. 1.1, а) преобразува определен набор от информационни елементи X, които влизат на входа, към определен набор на изхода Y. Ако множествата X и Y са крайни и дискретни, т.е. трансформацията се извършва в дискретни времена, тогава такива преобразуватели на информация се наричат ​​крайни преобразуватели. Елементите на множествата X и Y в този случай са предварително кодирани с двоични кодове и се изгражда трансформация на едно множество в друго.

Резултатът от трансформацията често зависи не само от това каква информация се е появила на входа в момента, но и от това, което се е случило преди това, тоест от историята на трансформацията. Например, една и съща информация - извинение от съсед, след като ви е настъпил в претъпкан автобус - ще предизвика у вас една реакция първия път и съвсем различна на петия път.

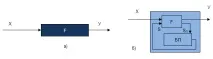
По този начин има по-сложни информационни трансформатори (ИТ), чиято реакция зависи не само от входните сигнали в момента, но и от това, което се е случило преди това, от историята на входа. Такива PI се наричат ​​автомати (схеми на паметта). В този случай се говори за автоматично преобразуване на информация (фиг. 1.1, б). Автоматът може да реагира различно на един и същ входен сигнал, в зависимост от състоянието, в което е бил. Автоматът променя състоянието си с всеки входен сигнал.

Нека да разгледаме няколко примера.

Пример 1 1 Карпов Ю.Г. Теория на автоматите-СПб.: Питър, 2003. Автомат, който описва поведението на "умен" баща.

Нека опишем поведението на баща, чийто син ходи на училище и носи двойки и петици. Бащата не иска да хваща колана всеки път, щом синът получи двойка, и избира по-фина родителска тактика. Ние дефинираме такъв автомат чрез граф, в който върховете съответстват на състояния, а дъгата от състояние s към състояние q, обозначена с x/y, се изчертава, когато автоматът от състояние s под въздействието на входен сигнал x преминава в състояние q с изходна реакция y. Графиката на автомата, симулиращ интелигентното поведение на родителя, е показана на фиг. 1.2. Този автомат има четири състояния, два входни сигнала - оценки и изходни сигнали, които ще интерпретираме като действия на родителя, както следва:

- вземете колан;

- да се скара на сина;

- успокоява сина;

- Надявам се;

- радвай се;

- радвай се.

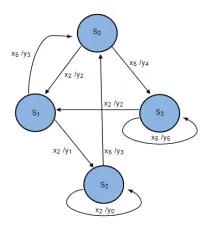
Син, който е получил една и съща оценка - двойка, очаква съвсем различна реакция от баща си у дома, в зависимост от произхода на обучението си. Например след третата двойка в историята синът ще бъде поздравен с колан, а в историята ще бъдат успокоени и т.н.

Машината на състоянието може да бъде реализирана както софтуерно, така и хардуерно. Софтуерното внедряване може да се извърши на всеки език от високо ниво по различни начини. Фигура 1.3 показва блокова диаграма на програмата, която реализира поведението на автомата от пример 1. Лесно се вижда, че топологията на блоковата диаграма на програмата повтаря топологията на графа на прехода на автомата. Всяко състояние е свързано с операцията NEXT, която изпълнява функцията на изчакване на следващото събитие на постъпване на нов входен сигнал и прочитането му в някакъв стандартен буфер x, както и последващ анализ на това какъв сигнал е той. В зависимост от това какъв сигнал е постъпил на входа, се изпълнява тази или онази функция и се извършва преход към ново състояние.

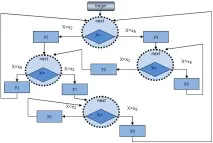
Хардуерната реализация на автомата ще бъде разгледана във втората част на този раздел.

Пример 2. "Студент"

Автоматът, чийто модел е показан на фиг. 1.4, описва поведението на ученика и учителя.

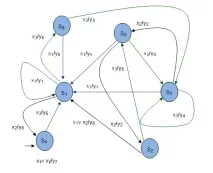
- държави;

- входни сигнали: "n", "2" и "5".

- изходни реакции:

• - знак "n";
• - успокояват;
• - хвалете ученика;
• - насърчават;
• - Надяваме се;
• - предупреждаваме;
• - приспадам;

Пример 3 1 . Електронен часовник (фиг. 1.5).

Електронните часовници с различни функционалности са едно от най-широко използваните електронни устройства в ежедневието, чието управление е изграденона базата на модел на краен автомат. Те обикновено показват: час, дата; имат функции като "настройване на час и дата", "хронометър", "будилник" и др. Опростена блокова схема на електронен часовник е показана на фигура 1.5

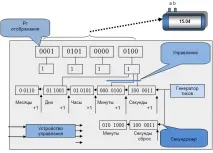
Регистрите показват или часа, или датата, или хронометъра, в зависимост от "Контрол". Устройството за управление е изградено на базата на модела на краен автомат. Машината отговаря на натискането на бутон "a" на кутията, като преминава в състояние "Set minutes", при което натискането на бутона "b" ще доведе до увеличаване на броя. Устройството за управление е изградено на базата на модел на краен автомат, чиято графика е показана на фиг. 1.6

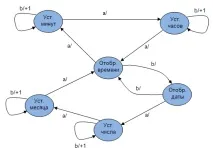
Така. От една страна, АВТОМАТИКАТА е устройство, което извършва някои действия без човешка намеса. От друга страна, AUTOMATIC е математически модел, който описва поведението на техническо устройство. В този случай реалното устройство, система и т.н. се разглежда като един вид "ЧЕРНА КУТИЯ" (фиг. 1.7).

Абстрактният автомат е математически модел, който описва техническо устройство чрез набор от входни, изходни сигнали и състояния, в допълнение:

• има много вътрешни състояния, наречени автоматни състояния;
• на входа на автомата постъпва краен набор от входни сигнали, има краен набор от изходни сигнали;
• зададена е преходната функция;
• зададена е функцията за формиране на изходите на автомата;
• определя се началното състояние на автомата.

Тоест, за да опишете автомата, трябва да използвате шестица от формата , където

• .

Автоматът реализира някакво преобразуване на набора от думи на входната азбука Z в набора от думи на изходната азбука W .

Автоматът се нарича краен,ако наборът от неговите вътрешни състояния и наборът от стойности на входните сигнали са крайни множества.

Автоматът се нарича синхронен, ако интервалът на времеви проби е постоянен, в противен случай се нарича асинхронен автомат.

Един автомат се нарича детерминиран, ако поведението на автомата във всеки момент от времето е уникално определено ( ,)

В зависимост от метода за определяне на изходния сигнал в синхронните автомати има:

---