Код на Шанън-Фано
Едно и също съобщение може да бъде кодирано по различни начини. Оптимално кодиран код е този, при който се изразходва минимално време за предаване на съобщение. Ако предаването на всеки елементарен знак (0 или 1) отнема едно и също време, тогава оптималният код ще бъде този, който ще има минималната възможна дължина.
Нека има случайна променлива X (x 1, x 2, x 3, x 4, x 5, x 6, x 7, x 8), имаща осем състояния с вероятностно разпределение
За да кодираме азбука от осем букви, без да отчитаме вероятностите с единен двоичен код, имаме нужда от три знака:
Това е 000, 001, 010, 011, 100, 101, 110, 111
За да отговорите дали този код е добър или не, трябва да го сравните с оптималната стойност, тоест да определите ентропията
След като определихме излишъкаLпо формулатаL =1- H / H 0 =1 - 2.75/3=0.084,виждаме, че е възможно да се намали дължината на кода с 8.4%.
Възниква въпросът: възможно ли е да се състави код, в който да има средно по-малко елементарни символи на буква.
Такива кодове съществуват. Това са кодовете на Шанън-Фано и Хъфман.
Принципът на конструиране на оптимални кодове:
1. Всеки елементарен знак трябва да носи максимално количество информация, за това е необходимо елементарните знаци (0 и 1) в кодирания текст да се срещат средно еднакво често. Ентропията в този случай ще бъде максимална.
2. Необходимо е на буквите от първичната азбука, които имат по-голяма вероятност, да бъдат присвоени по-кратки кодови думи от вторичната азбука.
Пример 2. Нека кодираме буквите от азбуката от пример 1 в кода на Шанън-Фано.
Всички букви се записват в низходящ ред на техните вероятности, след което се разделят на еднакво вероятни групи, коитоозначени с 0 и 1, след това отново разделени на равновероятни групи и т.н. (виж таблица 4.1)
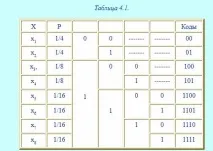
Средната дължина на получения код ще бъде равна на
И така, получихме оптималния код. Дължината на този код съвпада с ентропията. Този код се оказа успешен, тъй като вероятностите бяха точно разделени на еднакво вероятни групи.
Да вземем 32 две букви от българската азбука. Честотите на тези букви са известни. Азбуката включва и интервал, чиято честота е 0,145. Методът на кодиране е представен в таблица 4.2.
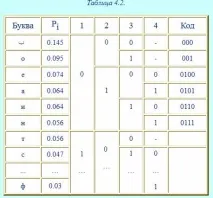
Средната дължина на този код ще бъде равна на, битове/буква;
Ентропия H =4,42 бита/буква. Ефективността на получения код може да се определи като съотношението на ентропията към средната дължина на кода. Равно е на 0,994. Когато стойността е равна на единица, кодът е оптимален. Ако кодираме с код с еднаква дължина, тогава ефективността ще бъде много по-ниска.