Коинтегриращ подход към търговията с двойки
Какво е коинтеграция?
(и защо не ни интересува толкова много корелацията)
Така че имаме две акции A и B и техните цени за определен период от време (ценови времеви редове). Цените на тези две акциище се наричат коинтегрирани, ако могат да бъдат линейно комбинирани в една серия със свойството стационарност.
Нека запишем това във формула. И тогава ще анализираме всичко по ред:
Но тъй като работим с голям набор от цени за определен период, а не за определен ден, цените на акции A и B се записват като:
След това казваме
"ако могат да бъдат линейно комбинирани".
Какво означава линеен?
За простота това е, когато добавяме „+“ или изваждаме „-“ цената на акция A от B или B от A. В този случай можем да умножим цените на една от акциите по някаква стойност. Както можете да видите във формулата, цената на акцията B се умножава по някакъв коефициент γ (няма да е съвсем вярно, но за простота ще нарека коефициента фиксирано число засега, въпреки че всъщност това е ненулев вектор). Така че извършваме проста манипулация с цените, умножаваме цените на акция B по някакво число и изваждаме тези цени от цените на акция A.
Нека да разгледаме по-подробно:
γ - изчислихме, че това число за тези дялове е 2. (Ще обсъдим как да изчислим по-долу). Всъщност този коефициент се нарича коефициент на коинтеграция.
Това се нарича линейна комбинация. Мисля, че го разбрахме.
„комбинирани в един ред“
„притежаващ свойството стационарност“
За простота: стационарността е, когато графиката постоянно обикаля една и съща стойност:
Неподвижен ред:
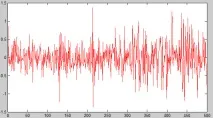
Нестационарни серии:
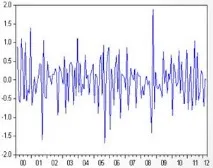
Стационарни:
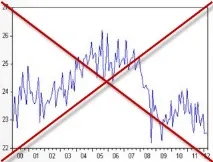
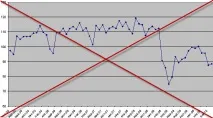
Нестационарни:
Казано правилно, стационарността е, когато вероятностните свойства са постоянни.
Защо за нас е важно да е неподвижен?
Да, защото движението му, както можете да видите от стационарните графики по-горе, е лесно за прогнозиране.
ВАЖНО!
Стационарността е статистическо свойство! И например, няма да наричаме такава сериястационарна :

Въпреки факта, чеможем да предвидим движението му (!).
ВАЖНО!
Далеч не всички двойки инструменти (акции, фючърси и т.н.) могат да бъдат коинтегрирани. Този имот има ограничен брой инструменти на пазара.
ВАЖНО!
За изчисляване на коинтеграцията е важно какъв период от време вземаме. И какъв срок. Това е, например:
Двойка: ISBC & STI е съвместно интегриран между 01.02.2012 г. и 01.03.2015 г. (чрез ежедневни затваряния). Но не е коинтегриран в интервала 01-01-2010 - 01-03-2015.
ВАЖНО!
Не без причина използвахме същия коефициент във формулата. Факт е, че самата разлика в цената ISBC - STI е същата като обичайните разлики на други двойки. Те нямат свойството стационарност (не се движат около една ос (линия)).
Как да определим коинтегрираната двойка и същия коефициент?
За това се използва тестът на Engle-Granger.
Стъпка 1. Определете дали цената (времевия ред от цени) на акция "А" за определен период от време е стационарна. Ако НЕ, тогава: Определете дали самите цени на акция "B" са стационарни. Ако НЕ, преминете към стъпка 2.
Стъпка 2. Изграждаме линейна регресия на двойката A и B и избираме остатъците (регресии в отделен ред.
Стъпка 3. Проверка на серията за стационарност"остатъци" на регресията, ако тя е стационарна, тогава двете серии от цени са коинтегрирани.
Сега по ред.
„Неподвижна ли е цената на акция „А“ за определен период от време.“
За да се определи дали дадена серия е стационарна (т.е. дали нейните вероятностни свойства се запазват във времето или с прости думи тя обикаля около определена линия или не), се използва тестът ADF (Augmented Dickey Fuller test). Той е най-популярният. За това как можете да се запознаете с него, ще посоча в края на статията.
За напреднали: липсата на стационарност е наличието на единичен корен I (1), тоест интеграция от първи ред. Наличието на стационарност е липсата на единичен корен I(0). Можете да го проверите с всеки тест за единичен корен.
"Изграждаме линейна регресия на двойката A и B и изолираме остатъците от регресията в отделен ред."
Регресията е просто търсене на връзка между два времеви реда. Тоест колко трябва да увеличите стойността на B, така че стойността на A да се увеличи с единица.
Помните ли оригиналния израз?
Ако преминем към дясната страна:
Това ще бъде регресионното уравнение. Нека да разгледаме по-отблизо.
Какво е регресия?
Пример за разбиране:
Имаме два реда данни:
- Дневни приходи на магазин за хранителни стоки за месец.
- Броят на хората, които влизат в магазина всеки ден в продължение на месец.
Очевидно е, че всеки човек харчи определена сума пари в магазина. Някои повече, други по-малко. Въпреки това, увеличаването на броя на купувачите почти винаги води до увеличаване на приходите. За да се определи как се променят средните приходи от броя на хората, които влизат, се съставя регресионно уравнение. Където основното нещо е крайният коефициент γ, който ще покажеколко средно ще се променят приходите, ако 1 допълнителен човек влезе в магазина.
Но тъй като намираме само „средна/средна“ стойност и всеки човек харчи различна сума пари в магазина, винаги ще имаме известно отклонение от прогнозираната стойност. Това означава, че дори точно 100 души да влизат в магазина на ден, приходите ще бъдат различни всеки ден, макар и да се колебаят около една и съща стойност. Тоест от 100 души можем да предвидим приходите от 100 хиляди рубли. Но един ден ще бъде 93 хиляди, друг 108 хиляди. Приходите са различни, но се движат около 100 хиляди.
Така че тази същата „грешка“ (разлика) на прогнозата и реално получените приходи се нарича регресионен остатък и се означава като:
И колкото по-добре сме изградили линеен регресионен модел (намерен е съответният коефициент γ). Колкото по-малко стойността на остатъка ще "ходи". Тоест толкова по-малко ще грешим в прогнозите си.
Линейната регресия се изгражда с помощта на метода на най-малките квадрати (OLS, на английски: OLS). Същността му е, че се търси еднаква стойност на коефициента γ, така че грешката (остатъкът) да е минимална.
Да продължим.
Така че имаме две акции A и B и техните цени за период от 2 години. Проведохме линейна регресия и видяхме, че средно връзката между цените на акциите може да се опише като:
Където μ е цената на акция A, ако цената на акция B е 0. Това е просто константа (число, което не се променя с времето, например може да бъде „3“ или „298“ или да бъде отрицателно).
За да проверим дали акциите са коинтегрирани или не, трябва да вземем отделно поредица от баланси за определен период от време, например 2 години. Въпреки че изчислихме катозапасите "средно" зависят един от друг, в продължение на 2 години цената, почти ежедневно, се отклонява от средната. Ние вземаме тези отклонения отделно и също така ги проверяваме за теста на ADF (проверете остатъците за стационарност). И ако тази серия е стационарна, тогава цените A и B са коинтегрирани.
Какво означава всичко това и как да търгувате?
Можем да предположим, че ако акциите се коинтегрират в рамките на 2 години (има някакъв баланс между техните стойности), тогава най-вероятно този баланс ще се поддържа и по-нататък. И можем да търгуваме с краткосрочни отклонения от това равновесие. Знаейки, че накрая ще стигнат до дългосрочното си равновесие. Какво означава отклонение от равновесието? Това са остатъците:
Тъй като тези отклонения са стационарни, можем да се надяваме, че след като се отклони от равновесието, остатъкът ще се върне към равновесната стойност.
Нека обясня отново със снимка. В идеалния случай графиката на остатъците трябва да изглежда така:

Както виждаме, отклонявайки се от 0, след известно време той постоянно се връща към него. Тоест стойността е лесно предвидима.
Стандартното внедряване на търговия изгражда търговия върху отклонение от z-резултат.
За да не претоварвам много статията, ще кажа само, че в статистиката има начин да се оцени разпространението на случайна променлива от нейната средна стойност, наречена дисперсия. Коренът на дисперсията се нарича стандартно отклонение и обикновено се записва като σ. Така че z-резултатът по същество измерва текущата стойност до равновесие в стандартни отклонения.
Типична диаграма z-резултат изглежда така:
Съответно изграждаме стратегия от тук:
-
ако Z-резултат≥2 (червена пунктирана линия отгоре) отваряне на къса позиция на A, дълга на B, където B се взема в размер, равен на коефициента γ, затваряне на позицията, когатоZ-резултат=0 (зелена пунктирана линия в средата);
Всичко на основата. Лимитът на z-резултат, от който се влиза, за някои двойки може да е повече, може да е по-малко, за да го определите, трябва да погледнете исторически данни.
Сега накратко за това как вече можете да докоснете методите за изчисление с ръцете си (ще трябва да го потърсите в Google):
-
За да създадете ADF и Engle-Granger, можете да използвате пакета EViews (можете да правите много интересни неща от иконометрията върху него).
Въпреки това е по-удобно да използвате пакета MATLAB или Rstudio (може да изтегля котировки директно от Yahoo и има вградена функция adf). Те също са удобни, защото например можете веднага да изчислите скоростта на връщане на спреда към равновесие. И съответно избирайте предварително акции с по-бърза конвергенция. Което означава повече и по-сигурен брой транзакции.
Можете също да изградите регресия в EXCEL, за това трябва да свържете пакет за анализ на данни.
Коинтеграционният подход, описан по-горе, вероятно е най-простият. Но това е само подход, даден за разбиране, макар и работещ. Усложнявам го за вас. Например регресията и стандартното отклонение трябва да се преизчисляват всеки ден, тоест прозорецът за изчисление трябва да се движи, за различните двойки размерът на прозореца може да е различен. OLS може да бъде заменен с Total или друг метод. Можете да работите предварително с ценови серии, за да получите по-точни записи. И филтрирайте самия спред. И много много други.
Също имапо-интересни динамични модели за изчисляване на входове, за в рамките на деня. И вероятностни подходи за статистически арбитраж, които в момента са в процес на тестване.