Координатни линии върху повърхнина на елипсоид - Студопедия
Класификация на криви върху повърхност
ГЕОМЕТРИЯ НА ЗЕМНИЯ ЕЛИСПОИД
На всяка повърхност, между две точки, можете да начертаете безкраен брой много различни линии, които имат определени свойства. За решаване на геодезични задачи върху повърхността на елипсоида ще се интересуваме само от онези линии от този набор, които са свързани с измервания, намалени до повърхността на елипсоида от физическата повърхност на Земята, както и координатни линии.
Имайки това предвид, разгледайте следните линии на повърхността на земния елипсоид.
Равнинни сечения – линии, образувани като следа от пресичането на повърхност с някаква равнина. В зависимост от това как сечещата равнина е ориентирана спрямо повърхността, има:нормални сечения в дадена точка, ако сечещата равнина съдържа нормалата към повърхността в дадена точка,централни сечения, когато равнината съдържа центъра на елипсоида, в този случай сечението винаги ще бъде нормално в екваториални точки. Ако нормалното сечение преминава по азимут, равен на 90 0 , то се наричапърви вертикал на елипсоида в дадена точка, чийто радиус еN,изразът на който е даден във формулата ( 3. 16 ).
Геодезическа линия е най-късата крива между две точки на повърхността. Трябва да се отбележи, че геодезичните линии на всяка повърхност играят специална роля (правите линии на равнината, дъгите от големи кръгове върху сферата и т.н.). Геометрията на геодезичните линии характеризира геометрията на повърхността и всички метрични проблеми върху повърхности се решават с помощта на уравнения, свързващи елементите на геодезичните линии. Пример за това са формулите на равнинната и сферичната тригонометрия, свързващи линейни иъглови елементи на геометрични фигури, образувани от прави линии върху равнината и големи дъги от кръгове върху сферата. Трябва да се отбележи, че на произволни повърхности, най-общо казано, няма подобни формули в затворена форма в елементарни функции, тук се използват диференциални формули на геодезични линии, чието интегриране позволява решаването на различни проблеми. В тези случаи се използват методи на диференциална геометрия на повърхности.
При решаване на геодезически задачи върху повърхността на земния елипсоид ще използваме методите на диференциалната геометрия.
За да разберем по-добре тези методи, използвани в сфероидната геодезия, нека си припомним основните елементи на кривите върху повърхностите. На първо място, припомняме, че в диференциалната геометрия се разграничаватправилни или гладки криви и повърхнини, които нямат особени (прекъснати) точки и линии. На такива линии и повърхности за текущата точка производната е непрекъсната и плавно променя стойността си с промяна на координатите. Такива криви и повърхности се наричат още диференцируеми. Повърхността на елипсоида е правилна и ще разгледаме геометрията на правилните криви на тази повърхност.
Нека си припомним основните определения, свързани с кривите върху повърхностите. Във всяка точка на кривата могат да се начертаят три взаимно перпендикулярни равнини и прави линии (фиг. 4.1), образуващисъпътстващия тристен на кривата :
-допирателна равнинаK към повърхността ивектор на допирателната към криватаLв точка M, имаща една обща точка с повърхността и кривата;
-нормална равнинаN, която е перпендикулярна на допирателната равнина - всички прави, лежащи в нормалната равнина и минаващи през точка M, се наричат вектори на нормали към кривата в тази точка,едната от които е перпендикулярна на допирателната равнина и се нарича нормала към повърхността в дадена точка;
-контактна равнина на криватаS, минаваща през три безкрайно близки точки на кривата, нормалният вектор, разположен в пресечната точка на нормалната и съседните равнини, се наричаглавна нормала на кривата;
-бинормален - нормален перпендикуляр на съседната равнина;
По този начин може да се отбележи, че всяка равнинна крива (и следователно равнинно сечение върху повърхност) има една съседна равнина. За геодезическа линия във всяка нейна точка главната нормала на кривата съвпада с нормалата към повърхността в дадена точка. За произволни криви на повърхности точките, в които тези два вектора съвпадат, се наричат геодезични точки. Ако нормален участък в дадена точка се начертае върху повърхността на елипсоид на въртене, тогава той също е геодезичен, точно както точка, разположена върху продължението на нормалното сечение към точка, лежаща на същия паралел с дадения, ще бъде геодезична. В централните сечения на елипсоида екваториалните точки са геодезични. По този начин може да се отбележи, че всяко нормално сечение на земния елипсоид има поне две геодезични точки, разстоянието между които ще бъде толкова по-голямо, колкото по-близо минава равнината на сечението от неговия център.


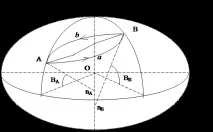
Ако на повърхността на елипсоида (фиг. 4. 2) имаме две точки A и B, тогава между тях е възможно да се начертае както геодезическа линия (една единствена линия), така и нормална линия както в едната, така и в другата точка на сечението. Ако тези точки не лежат на един и същ паралел ( BA ≠ BB ), което най-често може да се случи на практика, тогава получаваме две взаимно нормални сечения AaB и BbA, равнините на които ще преминават: за право нормално сечение в точка A -през т. B и нормалата AnA, за пряко нормално сечение в т. B - през т. A и нормалата BnB. Тези сечения не съвпадат помежду си, тъй като нормалите към повърхността на елипсоида AnA и BnB в тези точки не лежат в една и съща равнина, а образуват коси линии. Това ясно се вижда от фигура 4. 2.
Уравнението на всяка повърхност може да бъде написано във векторна форма
,( 4. 1 )
 |
като заместим тук изразите за координатите ( 3. 14 ) или ( 3. 15 ) за елипсоида, получаваме уравненията на неговата повърхност във функцията на параметричните координати:
( 4. 2 )
За всяка крива на повърхността можем да напишем уравнение в диференциална форма, което изразява линеен елемент от повърхността.
,
или в параметрични координати
.( 4. 3 )
Уравнение ( 4.3 ) се нарича първата основна квадратична форма на Гаус за всяка повърхност, чиито коефициентиE, F, Gимат изрази в частни производни:
( 4. 4 )
За ортогонална координатна мрежа върху повърхността на елипсоид (меридиани и паралели) винаги имаF = 0, което е лесно да се провери, ако имаме предвид уравненията ( 3. 14 ) или ( 3. 15 ), от които освен това получаваме изразите
.( 4. 5 )
Като се има предвид това, линейният елемент на повърхността на елипсоида има израз.
,( 4. 6 )
тук са приети обозначенията на коефициентите на първата квадратна форма за елипсоидаE = M 2 , G = r 2и техните изрази следват от уравненията (4.5). Геометричното значение на тези коефициенти ще бъде обяснено малко по-нататък.
Както беше отбелязано по-рано, координатните линии на повърхността на земния елипсоид са меридианите и паралелите, уравненията на коитоможе да се получи от уравнение (4.6), дадено (4.5). Ако приемемL = const,dL = 0, получаваме уравнението на меридиана като функция на геодезическата и намалената географска ширина
( 4. 7 )
И за паралела получаваме подобно при условиетоB = const, dB = 0
( 4. 8 )
В израза ( 4.7 ) и по-нататък използваме приетото в геодезията обозначение на функциятаV. Тази стойност се нарича втората основна функция на географската ширина и има следните изрази.
( 4. 9 )
Сравнявайки изразите ( 4. 6 ), ( 4. 7 ) и ( 4. 8 ), забелязваме, че стойносттаMизразява радиуса на кривината на меридиана, аr- паралелите.
Като се има предвид горното, отбелязваме, че меридианите и паралелите на земния елипсоид са плоски участъци. В този случай меридианите са нормални участъци, състоящи се изцяло от геодезични точки, следователно те също са геодезични линии. Имайте предвид, че геодезичните линии на елипсоида, минаващи по произволен азимут, не са плоски криви. Меридиан е изключение. Паралелите на земния елипсоид са плоски участъци, наклонени спрямо нормалата. Освен това, изразявайки радиуса на успоредникаrпо отношение на радиуса на първия вертикалN( 3. 16 ), забелязваме ъгъла на наклона на равнината на успоредника спрямо нормалата, която лежи в равнината на първия вертикал, равен на геодезическата ширинаВ.
( 4. 10 )
В този случай уравнение от вида (4.10) установява връзка между радиусите на кривина на наклонени и нормални равнинни сечения и изразяватеоремата на Мьоние.
Може да се отбележи, че паралелът с най-голям радиус (екваторът) е нормално сечение и геодезическа линия.
В теорията на повърхностите координатни решетки под формата на меридиани и паралели, когато една координатнаедна линия е геодезична, а другата негеодезична се нарича полугеодезична.
Не намерихте това, което търсихте? Използвайте търсачката:
Деактивирайте adBlock! и обновете страницата (F5)наистина е необходимо