Коригиращи кодове
Коригиращите кодове се наричат кодове, които позволяват да се откриват и коригират грешки от приемащата страна, без да се прибягва до повторно предаване на грешни кодови комбинации.
Въз основа на основните параметри и методи за кодиране и декодиране, коригиращите кодове могат да бъдат разделени преди всичко на блокови и непрекъснати.
Блоковите кодове се характеризират с това, че всяка кодова комбинация се състои от две части (блокове), първата се състои от информационни символи, втората се състои от контролни символи. Характеристика на непрекъснатите кодове е, че кодовата комбинация не е разделена на блокове, а контролните знаци се поставят според определено правило между информационните знаци.
За корекционните кодове, неравенството
N=Km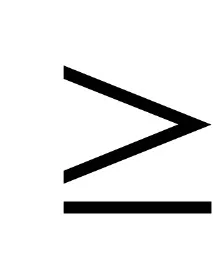
къдетоMе броят на съобщенията;Nе броят на кодовите комбинации;Kе основата на кода;
m– дължина на кодовата дума:m=n+k;n– брой информационни битове,k– брой контролни битове, които осигуряват локализиране и коригиране на изкривени елементи на кодова дума.
Броят на контролните битове, необходими за откриване и коригиране на единични грешки, се определя от следното разсъждение. При предаване на някое отMсъобщенията, всеки отmелементите на кодовата комбинация може да бъде изкривен или съобщението ще бъде предадено правилно. Следователно са възможниm+ 1резултати. С помощта на k контролни цифри е необходимо да се прави разлика между всички тези резултати. С помощта на k бита могат да бъдат кодирани 2 k резултата. Следователно условието трябва да бъде изпълнено
Например, акоM = 10, тогава в съответствие с равенствотоM=Knполучавамеn3,3 = 4. За да можете да откриете грешникодови комбинации и ги коригирайте, добаветеkконтролни цифри в съответствие с израза:
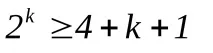
Когато равенството е изпълнено, получаваме
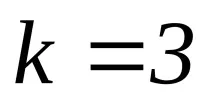
В този случай излишъкът на кода ще бъде
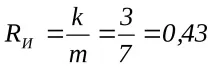
Кодовете за откриване на грешки трябва да имат кодово разстояниеd= 2. Нека определим какво трябва да бъде кодовото разстояние на коригиращите кодове. В този случай поставяме условието, че в една кодова комбинация не може да се появи повече от една грешка. Изразът за определяне на кодовото разстояние ще изглежда така:
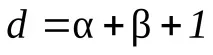
къдетоαе множеството открити грешки,
β– множество поправими грешки,
1– кодово разстояние за оптимален код;
Разгледайте тази формула на примера на единен трицифрен код.
Заα =0,β = 0d= 1. Този резултат съответства на единен оптимален код. Неговите кодови думи са:000, 001, 010, 100, 110, 101, 011, 111.
В този случай излишъкът на кода е равен на
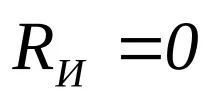
Заα = 1,β = 0d= 2. Този резултат съответства на единен код, който открива една грешка. Неговите кодови комбинации са:001, 010, 101, 110.
В този случай излишъкът на кода е равен на .
Заα = 1,β = 1d= 3. Този резултат съответства на единен оптимален код. Неговите кодови комбинации са:000, 111.
В този случай излишъкът на кода е равен на .
Общ алгоритъм за изграждане на блокови кодове, коригиращи единични грешки
В зависимост от необходимата битова дълбочина на кода се записва матрицата на идентичност(n

Тази матрица може да се използва за записване на всичкикомбинации от n-битов оптимален код.
За да се формира код, който коригира една грешка въз основа на тази матрица, е необходимо да се разшири доmцифри, т.е.(n


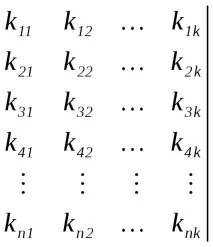
Получената матрица се нарича генерираща. Чрез модулно сумиране на 2 реда от тази матрица може да се получи единен код за излишък. В този код информационната и служебната част са разделени, поради което такъв код се нарича систематичен.
Към матрицатаAса наложени следните изисквания:
Тъй като ще бъде синтезиран излишен унифициран систематичен код, който позволява откриване и коригиране на единична грешка, разстоянието между кодовите комбинации трябва да бъде:d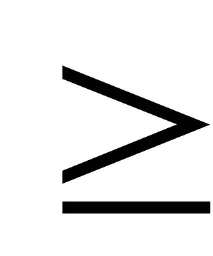
Разликата между редовете в приписаната матрица трябва да бъде поне(d- 2)цифри, тъй като вече има разлика в матрицата на идентичност в двата реда.
Предаваните кодови комбинации от приемащата страна трябва да бъдат обект на контрол, за да се открие наличието или отсъствието на грешка навсякъде в кодовата комбинация. За да направите това, от приемащата страна се използва матрица за проверка, чиято задача е да открие грешка и да посочи нейното местоположение.
Матрицата за проверка се изгражда по следния начин: на матрицата за идентичностk

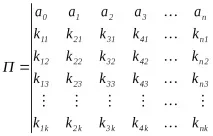
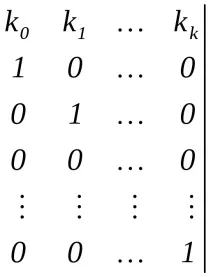
Към матрицатаПе представено следното изискване.
Сумата от единици по модул2на който и да е ред от контролната матрица трябва да бъде четно число (или нечетно във всички редове), тъй като сума по модул2е равна на нула за четен паритет. Това е условие за откриване и локализиране на грешка във всяка кодова комбинация. Локализацията на грешката се основава на индивидуална кодова дума (идентификатори) и тази кодова дума е представена като
Пример: искате да изградите систематичен код, който ви позволява да откриете грешното показване на което и да е число от0до9на седемсегментен дисплей и да го коригирате.
Според условието на проблема, броят на показаните числа (съобщения)M = 10. За представяне на тези числаn= 4,k= 3. Нека създадем генерираща матрица.

Условието е изпълнено: най-малко(d-1)единици. Въз основа на тази матрица можете да изграждате16кодови комбинации с битова дълбочина. Нека съставим10кодови комбинации, които ще са необходими за посочване на необходимите числа. Нека да са следните комбинации:

Първите четири кодови комбинации са редовете на матрица A. Последните 6 кодови комбинации са сумите от редове по модул2, съответно: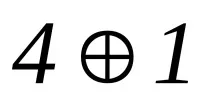
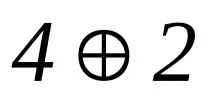
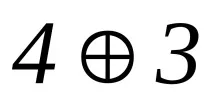
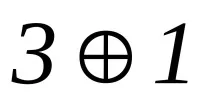
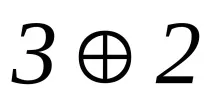
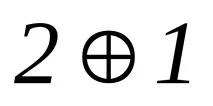
Изграждане на чекова матрица

Въз основа на матрицата за проверка е възможно да се съставят уравнения за идентификационни кодове за местоположение на грешка:
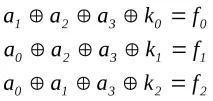
Последователносттаf0f1f2– е кодът на грешна или безгрешна комбинация
Ако кодовата комбинация не съдържа грешки, тогава според (*) всички позиции ще съдържат нули, следователно кодът ще бъдеf0f1f2= 0 0 0.
Помислете за подчертаната кодова комбинация1 0 1 0 1 0 1и започнете да въвеждате грешките последователно.
Въвеждаме грешка в битa0и получаваме кода на идентификатора на грешката в този бит:
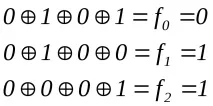
След това въвеждаме грешка в бита1и получаваме кода на идентификатора на грешката в този бит; след това въвеждаме грешкатаа2и получаваме кода на идентификатора на грешката в този бит и т.н.
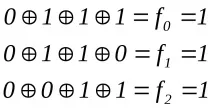
В резултат на това получаваме таблица с кодове за идентифициране на грешки:
Да проверим резултата. Нека комбинацията1000011бъде предадена и приемете1001011. Определете кода на идентификатора:
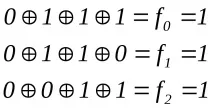

Недостатъкът на този метод е, че кодовете за идентифициране на грешки не съответстват на десетичните числа.