Криптиране на съобщения чрез различни методи
Помислете как да шифровате съобщение, като използвате метода на заместване (с други думи, метода на заместване). Първо, използваме шифъра на Цезар. Да предположим, че искаме да шифроваме съобщението "WHERE IS ABBA".
Както е известно, цикличният шифър на Цезар се получава чрез замяна на всяка буква от открития текст с букви от същата азбука, разположени отпред след определен брой позиции, например след три позиции. Нарича се цикличен, защото при извършване на замяната последната буква от азбуката отново е последвана от първата буква от азбуката. Нека да запишем фрагментите от българската азбука и да покажем как се извършва криптирането (редът на заместване):
В резултат на трансформацията ще се получи шифрограма:
В този случай ключът е количеството отместване (броят позиции между буквите). Броят на ключовете на този шифър е малък (равен е на броя на буквите от азбуката). Не е трудно да се отвори такъв шифър чрез изброяване на всички възможни ключове. Недостатъкът на шифъра на Цезар е неговата ниска криптографска сила. Това се обяснява с факта, че в шифрования текст буквите все още са подредени по азбучен ред, само произходът е изместен с няколко позиции.
Замяната може да се извърши със знаци от друга азбука и с по-сложен ключ (алгоритъм за заместване). За простота отново даваме само началните части на азбуките. Редовете показват реда, в който буквите от българската азбука се заменят с буквите от латинската азбука. Нека шифроваме фразата "WHERE IS ABBA":
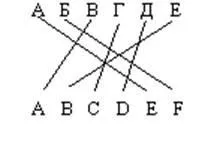
В резултат на такова криптиране ще се получи криптограма:
По-рационално е да напишете използвания в последния случай ключ под формата на таблица:
При криптиране буквите могат да бъдат заменени с цифри (в най-простия случай с поредни номера на буквите в азбуката). Тогава нашето криптиране ще изглежда така:
Замяната на знаци в обикновен текст можесе появяват на специални символи, например на „танцуващи мъже“, както в историята на К. Дойл, или с помощта на знамена, както се прави от моряците.
Афинните криптосистеми имат по-висока криптографска сила в сравнение с шифъра на Цезар.
В афинните криптосистеми, поради математически трансформации, буквите, които заместват обикновения текст, се смесват на случаен принцип. В афинните криптосистеми буквите в обикновен текст се номерират с цифри, например за кирилица от 0 до 32. След това всяка буква в обикновен текст се заменя с буква, чийто пореден номер се изчислява с помощта на линейно уравнение и изчисляване на остатъка от целочислено деление.
Афинните криптосистеми се дефинират с помощта на две числа a и b. За българската азбука тези числа са избрани от условието a ≥ 0, b ≤ 32. Максималният брой знаци в използваната азбука е означен с g. Освен това числата a и g = 33 трябва да са взаимно прости. Ако това условие не е изпълнено, тогава две различни букви могат да бъдат показани (превърнати) в една. Всеки буквен код m в обикновен текст се заменя с буквения код на криптограмата съгласно следното правило. Първо се изчислява числотоa = a×m + b, след което се извършва целочисленото деление на числотоa на числото g = 33, т.е.
a = b(mod (g)). Остатъкът от целочисленото деление b се използва като символен код на шифрограмата.
За категоричност избираме следните числа: a = 5 и b =3.
В таблицата е даден фрагмент от процедурата, илюстриращ реда на криптиране.
В шифрите, които разгледахме по-рано, всяка буква от открития текст съответства на една конкретна буква от криптограмата. Такива шифри се наричат едноазбучни заместващи шифри.
Дълги съобщения, получени по метода на едноазбучно заместване (друго име е прост шифъреднобуквена замяна) се разкриват с помощта на таблици с относителни честоти. За целта се изчислява честотата на срещане на всеки знак, разделена на общия брой знаци в шифрования текст. След това, използвайки таблицата на относителните честоти, се определя коя замяна е направена по време на криптирането.
Полиазбучните заместващи шифри (или полисемантичните заместващи шифри) позволяват увеличаване на криптографската сила. В този случай на всеки знак от отворената азбука се присвояват не един, а няколко знака за криптиране.
По-долу е даден фрагмент от полиазбучния заместващ ключ:
Използвайки полиазбучен шифър, съобщението „WHERE IS ABBA“ може да бъде криптирано по няколко начина:
10-99-15-12-4-14-12 и др.
За всяка буква от оригиналната азбука се създава определен набор от символи на шифрограмата, така че наборите от всяка буква да не съдържат едни и същи елементи. Полиазбучните шифри променят картината на статистическите честоти на появата на буквите и по този начин затрудняват отварянето на шифъра без познаване на ключа.
Помислете за друг полиазбучен заместващ шифър, който е описан през 1585 г. от френския дипломат Блез дьо Виженер. Криптирането се извършва с помощта на така наречената таблица на Виженер. Тук, както и преди, е показана само част от таблицата, за да се представи само идеята на метода.
Всеки ред в тази таблица съответства на един прост заместващ шифър (като шифър на Цезар). При криптирането отвореното съобщение се записва в низ, а ключът се поставя под него. Ако ключът е по-кратък от съобщението, тогава ключът се циклизира. Криптирането се получава чрез намиране на символа в матрицата от букви на шифрограмата. Символът на шифрования текст се намира в пресечната точка на колоната с буквата на открития текст и реда със съответната буква на ключа.

Да предположим, че искаме да шифроваме съобщението "WHERE IS ABBA". като ключДа изберем думата "ДЕВА". В резултат на това получаваме:
В резултат на трансформациите ще се получи криптиране
Системата Playfair създава полиазбучни шифри. Помислете за основната идея на тази система.
Криптирането се извършва с помощта на квадрат (или правоъгълник), в който се въвеждат буквите от съответната национална азбука. Буквите се изписват в квадрат или правоъгълник в произволен ред. Тази конфигурация на реда и таблицата е секретният ключ. За категоричност, нека вземем правоъгълна маса с размери 8x4, кирилица като буквите от азбуката и подредим буквите по азбучен ред. Тъй като броят на българските букви е 33, а броят на клетките е 32, ще изключим буквата Y от таблицата.
Да предположим, че искате да шифровате думата КРИПТОГРАФИЯ.
Помислете за правилата за криптиране.
1. Чистият текст е разделен на блокове от две букви. Буквите в едно и също поле не трябва да са еднакви. Нека разделим оригиналната дума на блокове от две букви KR-IP-TO-GR-AF-IA.
2. Ако буквите от шифрования текст са в различни редове и колони, тогава буквите, разположени в ъглите на правоъгълника, обхващащ буквите от открития текст, се използват като заместващи букви. Например блокът KP се заменя със знаците IT.
3. Ако буквите на открития текст попадат в един ред, тогава шифрограмата се получава чрез циклично изместване надясно с една клетка. Например IP блокът ще бъде преобразуван в YI. Друг пример за това правило. Ако, да предположим, се изисква да се преобразува блокът KN, тогава получаваме LO.
4. Ако и двете букви от обикновения текст попадат в една колона, тогава за криптиране се извършва циклично изместване с една клетка надолу.
Блокът ZhC ще бъде преобразуван в символи OY, а блокът Tb в символи bB.
В съответствие с описаните правила думата КРИПТОГРАФИЯ ще бъдепреобразуван в криптограма ITYITSKAUDPSH.
Имайте предвид, че ако блоковете с обикновен текст се състоят от едни и същи букви, тогава криптограмата също ще съдържа същите двойки знаци. По тази причина разглежданият шифър е едноазбучен. Модифицирането на този шифър обаче го превръща в полиазбучна система. За това се използват няколко Playfair маси и се извършва многократно криптиране.
Тук е подходящо да разгледаме криптографската система на Hill, в която криптирането се извършва с помощта на математически трансформации: изчисления с помощта на техники на линейна алгебра [4].
Този шифър за една буква може да се счита за полиазбучен. Двойките букви обаче са криптирани навсякъде по един и същи начин. Следователно, в широкия смисъл на термина, криптографската система на Хил трябва да се припише на едноазбучни шифри.
Първоначално обикновеният текст трябва да се преобразува в набор от числа, като се използва методът на заместване. Да предположим, че текстът е криптиран, написан с 26 латински букви. Избираме следния алгоритъм за замяна на буквите с цифри: латинските букви A, B, C, D, …, Z ще заменим съответно с цифрите 1, 2, 3, 4, …, 26. С други думи: номерираме буквите по реда на подреждането им в азбуката, а при замяната ще използваме техните поредни номера. В случая е избран такъв алгоритъм за заместване, но е ясно, че той може да бъде всякакъв.
Да предположим, че трябва да шифроваме немската дума ZEIT. Нека заменим буквите в съответствие с техните поредни номера в азбуката с четири числа: 26 - 5 - 9 - 20.
След това трябва да изберете някакво число d ≥ 2. Това число показва реда на разделяне на обикновения текст в група от знаци (определя колко букви ще има във всяка група). От математическа гледна точка числото d показва колко реда трябва да има във векторите -колони. Да вземем d = 2. Това означава, че числата 26 - 5 - 9 - 20 трябва да бъдат разделени на групи от две букви (две числа) във всяка група и записани като колонни вектори:

В резултат на криптирането по комуникационния канал ще бъде изпратена поредица от числа: 19 - 22 - 24 - 3. За предварително избрания заместващ ключ това ще съответства на шифъра SVXC. Този пример илюстрира факта, че системите за криптиране често се основават на математически трансформации.