Кръстосани линии
Вижте също:- Взаимно перпендикулярни линии
- Взаимно перпендикулярни прави
- Взаимно разположение на две прави в равнина Разгледайте две прави, дадени от уравненията и .
- Ако линиите не се пресичат и не са успоредни една на друга, тогава пресечната точка на техните проекции със същото име не лежи на една и съща комуникационна линия.
- Световни финансови потоци. Преките чуждестранни инвестиции в България.
- Косвени методи
- Непряко разсъждение на пропозиционалната логика
- Успоредни прави линии.
- Успоредни прави линии.
- Пресичащи се линии.
- Портфейлни и преки инвестиции
- Проективно пространство, неговите равнини и прави.
Пресичащите се прави са две прави, които не лежат в една равнина.
Ако линиите не се пресичат и не са успоредни една на друга, тогава пресечната точка на техните проекции със същото име не лежи на една и съща комуникационна линия.
Пресечната точка на фронталните проекции на правите (фиг. 28) съответства на две точки A и B, от които едната принадлежи на правата a, другата на. Техните фронтални проекции съвпадат само защото в пространството двете точки А и В са на общ перпендикуляр на равнината на фронталната проекция. Хоризонталната проекция на този перпендикуляр, обозначена със стрелка, ви позволява да определите коя от двете точки е по-близо до наблюдателя. В предложения пример точката B, разположена на правата c, е по-близо, следователно правата в минава на това място по-близо до правата a и фронталната проекция на точка B затваря проекцията на точка A. (За точки C и D решението е подобно).
Този метод за определяне на видимостта се основава на конкурентни точки. В този случай точки A и B се конкурират фронтално, а C и D се конкурират хоризонтално.
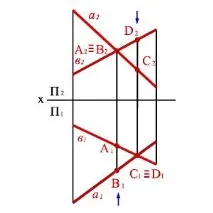
Фигура 28. Кръстосани линии
| следваща лекция ==> | ||
| успоредни прави линии | Проекции на равнинен ъгъл |