Курсова работа Структурни автомати
1. Основни понятия. Каноничен метод за структурен синтез на автомати. Теорема на Глушков за структурната пълнота
2. Основни етапи на каноничния метод на структурния синтез
2.1 Кодиране на автоматни азбуки
2.2 Избор на елементи от паметта на автомата
2.3 Избор на функционално завършена система от логически елементи
2.4 Конструиране на уравнения за булеви функции на възбуждане и автоматни изходи
2.5 Построяване на функционална схема на машината
3. Пример за каноничен метод на структурен синтез
4. Елементи на паметта
4.1 Елементи на паметта с един информационен вход
4.2 Елементи на паметта с два информационни входа
4.3 Преходна матрица на запаметяващ елемент
5. Кодиране на състояния и изходи на автомати и сложност
6. Осигуряване на стабилност на функционирането на цифровите машини. Състезание с коли
6.1 Методи за елиминиране на състезания в слот машини
Темата на курсовата работа "Структурни автомати" в дисциплината "Приложна теория на управлението на автомати".
- основни понятия за структурни автомати;
- каноничен метод за структурен синтез на автомати;
- теорема на Глушков за структурната пълнота;
- основните етапи на каноничния метод на структурния синтез;
- примери за каноничния метод на структурен синтез;
- кодиране на състоянията и изходите на автомата и сложността на комбинационните схеми;
- осигуряване на стабилност на функционирането на цифровите машини;
- състезания в машините;
- методи за премахване на състезания в автомати и др.
1.Основни понятия. Каноничен метод за структурен синтез на автомати. Теорема на Глушков за структурна пълнота
След етапа на абстрактен синтез на автомати,завършвайки с минимизиране на броя на състоянията, следва етапът на структурния синтез, чиято верига е изграждането на схема, която реализира автомата от логически елементи от даден тип.
Ако абстрактният автомат беше само математически модел на дискретна система, тогава структурният автомат отчита структурата на входните и изходните сигнали на автомата, както и неговата вътрешна структура на ниво блокови диаграми. Структурният синтез се извършва от структурната теория на автоматите, чиято основна задача е да намери общи методи за конструиране на структурни диаграми на автомати въз основа на състава на елементарни автомати, принадлежащи към предварително определен краен брой типове.
Съставът на елементарните автомати в общия случай се разбира по следния начин.
Нека са дадени елементарни автомати S1. ск. Нека обединим елементарните автомати в система от съвместно работещи автомати. Нека въведем под внимание някакъв краен набор от възли, наречени външни входни и външни изходни възли. Тези възли се различават от възлите на разглежданите елементарни автомати, които се наричат вътрешни. Съставът на автомата е този в получената система от елементарни автомати S1 . Sk и външни възли, някои възли (както външни, така и вътрешни) са идентифицирани. От гледна точка на съвместната работа на система от автомати, смисълът на операцията за идентифициране на възли е, че елементарен сигнал, попадащ на един от възлите, включени в набора от възли, идентифицирани един с друг, по този начин попада върху всички възли на този набор. Ще приемем, че автоматите, включени в схемата на автомата, работят заедно, ако във всеки момент от времето на автомата е включеновсички външни входни възли се доставят с набор от входни сигнали (структурен входен сигнал на веригата) и набор от изходни сигнали (структурен изходен сигнал) се премахва от всички външни изходни възли.
В структурната теория се счита, че входните и изходните канали се състоят от елементарни входни (изходни) канали. По всички елементарни входни (изходни) канали могат да се предават само елементарни сигнали.

Фигура 1 - Структурен автомат
Наборът от възможни стойности на сигнали, приложени към един външен входен (изходен) възел, се нарича структурна входна (изходна) азбука на автомата. Азбуката трябва да е окончателна.
Входните и изходните сигнали се дават от крайни подредени набори от елементарни сигнали, наречени вектори, а елементарните сигнали, които ги съставят, са компоненти на вектори. Броят на векторните компоненти е размерът на азбуката.
Например, X=1, x2, x3, x4, x5 > е входната азбука на абстрактния автомат.
Структурна входна азбука, чийто размер е равен на три:
Векторното представяне на входния и изходния сигнал се нарича съответно структуриран входно-изходен сигнал.
Предполага се, че всички автомати, включени в композицията, имат една и съща структурна азбука и работят в едно и също автоматно време. В момента най-разпространената структурна азбука е двоичната, което се обяснява с простотата на нейното представяне в съвременните елементи и устройства. В допълнение, за двоичната азбука, апаратът на булевите функции е най-развит, което позволява формално извършване на много операции във веригата. Ето защо в бъдеще при решаването на задачи за структурен синтез на автомати ще използваме основно двоичната, структурна азбука.
Да приемем, че във всякамомента на времето на автомата, структурният изходен сигнал на веригата се определя еднозначно от крайната последователност от структурни входни сигнали, получени до този момент, началните състояния на автоматите, включени във веригата, и идентификациите на възлите, направени по време на изграждането на веригата. В този случай построената схема ще се разглежда като някакъв автомат S, а самата верига ще се нарича структурна диаграма на този автомат.
Построеният по този начин автомат S е резултат от композиция на елементарни автомати S1. ск. За разлика от абстрактния C-автомат, който има един вход и два изходни канала, които приемат сигнали във входната и изходната азбука на автомата, структурният автомат има входни и изходни канали, на които се появяват сигнали в структурната азбука на автомата. В случай на двоична азбука, всеки входен и изходен сигнал на абстрактен автомат може да бъде кодиран съответно от вектори с различна дължина, чиито компоненти приемат две стойности - нула и една.
На етапа на структурния синтез се избират предварително елементарни автомати, от които след това чрез техния състав се изгражда структурна диаграма на автомата на Мили, Мур или С, получена на етапа на абстрактен синтез. Ако съществува решение на задача за структурен синтез, се казва, че дадената система от автомати е структурно завършена.
Понастоящем няма ефективни методи (много по-прости от метода за изброяване на всички опции) за решаване на основния проблем на структурния синтез за всеки набор от структурно пълни системи от елементарни автомати. Следователно обикновено се използва така нареченият каноничен метод на структурен синтез, при който се използват елементарни автомати от някакъв специален вид: автомати с памет, имаща повече от едно състояние, и автоматибез памет - с едно състояние. Автоматите от първия клас се наричат елементи на паметта, а автоматите от втория клас се наричат комбинационни или логически елементи.
Теоретичното обосноваване на каноничния метод за структурен синтез на автомати е теоремата за структурната пълнота, доказана в (теорема на Глушков):
Всяка система от елементарни автомати, която съдържа автомат на Мур с нетривиална памет, пълна система от преходи и пълна система от изходи, както и всяка функционално пълна система от логически елементи, е структурно завършена.
Съществува обща конструктивна техника (каноничният метод на структурен синтез), която в разглеждания случай позволява да се намали проблемът за структурния синтез на произволни автомати до проблема за синтеза на комбинационни схеми.
Резултатът от каноничния метод на структурния синтез е система от логически уравнения, която изразява зависимостта на изходните сигнали на автомата (функцията на изходите на автомата) и сигналите, подавани към входовете на елементите на паметта, от сигналите, идващи на входа на целия автомат като цяло, и сигналите, взети от изхода на елементите на паметта (функцията на възбуждане на елементите на паметта на автомата). Тези уравнения се наричат канонични.
За правилната работа на веригите е очевидно невъзможно да се позволи на сигналите на входа на запаметяващите елементи да участват директно във формирането на изходни сигнали, които да се подават през веригите за обратна връзка едновременно към тези входове. В тази връзка елементите за съхранение не трябва да бъдат автомати на Mealy, а автомати на Moore (вижте уравненията за функционирането на тези автомати).
По този начин една структурно пълна система от елементарни автомати трябва да съдържа поне един автомат на Мур. В същото време, за синтеза на всякакви автомати с минимален бройелементи на паметта, като такива елементи е необходимо да се изберат автомати на Мур, притежаващи пълна система от преходи и пълна система от изходи - така наречените пълни автомати.
Помислете за пълнотата на автоматите на паметта, като използвате автомата на Мур като пример. (Таблица 1.) Пълнотата на преходната система означава, че за всяка двойка състояния (am , ..., as ) на автомата има входен сигнал, който превежда първия елемент от тази двойка am във втория - as, т.е. в такъв автомат във всяка колона на таблицата за преход трябва да се появят всички състояния на автомата. Пълнотата на изходната система на автомата на Мур се състои в това, че на всяко състояние на автомата се присвоява собствен специален изходен сигнал, който е различен от изходните сигнали на други състояния.
Очевидно в такъв автомат броят на изходните сигнали е равен на броя на състоянията на автомата. Заедно с предишното твърдение, това води до факта, че в автомат на Мур с пълна система от изходи, може да се идентифицират състоянията на автомата с неговите изходни сигнали. В тази връзка в автоматите на паметта ще използваме една и съща нотация както за състояния, така и за изходни сигнали, т.е. маркираната таблица на прехода в автоматите на Мур с пълна система от изходи се превръща в проста таблица на прехода. Машина на Мур в табл. 1. отговаря на условията за завършеност на системата от преходи и изходи.
Наличието на функционално завършена система от логически елементи прави възможно реализирането на булева функция с всякаква степен на сложност.
След като изберете елементите на паметта икодиране на състоянието, синтезът на структурен автомат се свежда до синтеза на комбинационна схема, която изпълнява канонични уравнения.
Автоматът на паметта може да се разглежда и на абстрактно и структурно ниво. Един абстрактн автомат с памет има един входен и един изходен канал. При преминаване от абстрактен автомат към структурен автомат входните и изходните сигнали трябва да бъдат кодирани от съответните двоични множества.
2.Основните етапи на каноничния метод на структурен синтез
Има няколко основни етапа в каноничния метод на структурен синтез:
1. Кодиране на автоматни азбуки.
2. Избор на памет елементи.
3. Избор на функционално завършена система от логически елементи.
4. Писане и минимизиране на канонични уравнения.
5. Построяване на функционална схема на автомата.
Началните данни за стартиране на този метод са абстрактен цифров автомат с памет, определен от таблица с преходи и изходи. Нека разгледаме по-подробно всеки от етапите на каноничния метод.
2.1 Автоматно азбучно кодиране
На структурно ниво всяка буква от входната азбука xX, всяка буква от изходната азбука yY и всяка буква от азбуката на състоянието aA се кодират от двоични вектори (двоични набори), чийто брой компоненти се определя, както следва:
където int е най-близкото по-голямо цяло число.
X, Y, A - силата на азбуката съответно на входа, изхода и състоянията. Кардиналността на една азбука е броят на отделните знаци в тази азбука.
Процесът на заместване на буквата от азбуката (X, Y, A) на абстрактен автомат с двоични вектори се нарича кодиране и се описва с кодиращи таблици. Таблицата за кодиране има следната форма: от лявата странаса изброени всички символи на абстрактната азбука, а вдясно - съответните им двоични вектори.
Абстрактният автомат на Mealy е даден от таблица с преходи и изходи (Таблица 2.). Извършете кодиране на автоматните азбуки.
| A \ X | x1 | x2 |
| a1 | a2 /y1 | a3 /y3 |
| a2 | a1 /y2 | a2 /y1 |
| a3 | a2 /y2 | a1 /y1 |
Нека напишем азбуките на автомата и определим дължините на векторите на кодовете на азбуките:
Попълнете кодовите таблици:
| x1 | 0 |
| x2 | 1 |
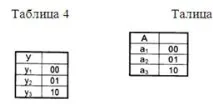
Получената таблица е структурната таблица на преходите и изходите на автомата (Таблица 6.) Получаването на структурната таблица на преходите - изходи на автомата завършва етапа на кодиране.