Квадратна или тетрагонална система
Квадратна или тетрагонална система- набор от кристали, в които може да се намери една (най-много) четирикратна ос на проста или сложна симетрия (вижте Кристалографски системи). В допълнение към една четворна ос, която е задължителна за тази система, може да има и по-голям брой елементи на симетрия: оси на симетрия от по-малък порядък (двоен), равнини на проста и сложна симетрия и център на симетрия. Четворната ос се приема катоглавнакристална ос и се обозначава с букватаc; две взаимно перпендикулярни и перпендикулярни на остаcдвойни оси, наречени. страничен кристален. брадви; те са равни една на друга, но повече или по-малко от главната ос, и двете се означават с букватаa[Освен това, в кристалите на квадратната система могат да бъдат начертани още две странични оси, които също лежат в основната равнина и образуват ъгъл от 45 ° със споменатите странични оси. Те назовават.междинниоси.]. Главната и страничните оси са подравнени с координатните (правоъгълни) оси. Кристал, чиито лица пресичат и трите координатни оси и същевременно две странични(XиY)на еднакво разстояние от началото, образува т.нар.главнаформа; неговото обозначение според Милър (111), според Науман Р. Равнината, в която страничните оси лежат, следователно, перпендикулярни на главнияc, се нарича основа или базопинакоид и се обозначава с 001 от Милър и 0P от Науман. Разпределението на различни физични свойства в тях е тясно свързано с общия характер на симетрията на кристалите от квадратната система. Така например, според съществуването тук на единична (четворна) ос на симетрия, която се приема като главна кристална ос, има самоеднапосока, по която не възниква двойно пречупване (виж. Двойно пречупване); съвпада сглавна осc. По този начин кристалите на квадратната системаса едноосниПриродата на топлопроводимостта (виж), подобно на скоростта на разпространение на светлината, може да бъде представена като сфероид, в който главната ос служи като ос на въртене; в резултат на това на равниниперпендикулярнинаглавната ос,топлопроводимостта се изразявакато кръг,върхудругикатокато елипса,което беше ясно доказано от Senarmont с фигури на топене. Разширението при нагряване се подчинява на същия общ характер: в посока на главната ос (и само на главната) има един (най-голям или най-малък) коефициент на разширение, във всички останали посоки - друг, еднакъв за всички посоки, които имат същия ъгъл с главната ос. В зависимост от това какви други елементи на симетрия присъстват, в допълнение към четворната ос на симетрия, квадратната система е разделена на седем класа или отдела, на които са дадени специални имена.
1)ХолоедрияКвадратната система съдържа кристали с най-симетрично разположение на лицата. Имат: четворна ос; четири двойни оси, сключващи ъгъл от 45° помежду си и разположени в равнина, перпендикулярна на четворната ос; център на симетрия; пет равнини на симетрия, минаващи през осите на симетрия - четири се пресичат по четворната ос (главната ос), а петата е перпендикулярна на тях. Те включват: дитрагонална бипирамида (октаедрична двойна пирамида, фиг. 1).
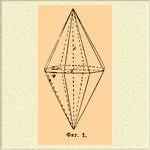
И трите параметъра на всяка равнина са различни и се изразяват в общата форма a:b:c. Ограничено до 16 равни триъгълни лица. Общ знак по Милър (hkl) и по Науман mPn. Тетрагонална бипирамида (квадратна пирамида) от 1-ви вид (фиг. 2).
Параметрите за страничните оси са еднакви, за главните - повече или по-малко; общ изглед - a: s. Ограничено до 8 равниравнобедрени триъгълници (означение hh 1 и mР). Тетрагоналната бипирамида (квадратна пирамида) от 2-ри вид е напълно подобна на външен вид на тази от 1-ви вид; разграничаването им един от друг е възможно само когато се срещнат заедно; в този случай те се завъртат една спрямо друга с 45 °, в това положение страничните оси на бипирамидата от 2-ри вид ще минават през средата на хоризонталните ребра (фиг. 3).
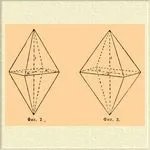
Знак: hol и mР∞. Според трите типа бипирамиди има форми на отваряне, при които страните са успоредни на главната осc; те назовават. призми: двуъгълна (осмиедърна) призма - знак (hko) и ∞Pn (фиг. 4); тетрагонална призма от 1-ви и 2-ри вид, различаващи се една от друга по същия начин, както се различават съответните бипирамиди (фиг. 5 призма от 1-ви вид).
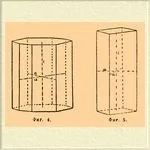
И накрая, последната форма на същия отдел е две равнини на основата, или базопинакоид, успоредни една на друга (виж фиг. 4 и 5o); знак (001) и oP.
2)Пирамидален(бипирамидален)хемиеедър.Има четирикратна ос на симетрия и равнина на симетрия, перпендикулярна на нея. Свързаните тук форми могат да бъдат изведени от формите от първи клас, ако си представим, че в двуъгълната пирамида двойки равнини, които се пресичат в средните ръбове, остават и изчезват на свой ред. По този начин се получава форма, която е напълно подобна на пирамида от 1-ви и 2-ри вид, но се различава от тях по позиция в пространството: в нея страничните оси свързват точки, разположенине в средата на страничните ребра; казва се кв. бипирамида от 3-ти вид; знакът на π(hkl) и π(mPn)/2. Действайки по същия начин с други холоедрични форми (намирайки в тях съответните цели равнини или части от равнини), ние получаваме само от диетрагонална призма нова форма, призма от 3-ти вид, напълно подобна на призмата1-ви и 2-ри вид, но се различават от тях по положение в пространството (както при пирамида от 3-ти вид); знакът на π(hko) и . Всички останали са холоедрични. формите според този тип хемиедрии не дават нови форми.
3)Трапецоедърен хемиедър.Има: четворна ос на симетрия и четири двойни оси на симетрия, пресичащи се под ъгъл от 45° и лежащи в равнина, перпендикулярна на първата. Това принадлежи на площада. трапецоедър (фиг. 6), който може да се получи от дитетрагонална пирамида чрез развитието и изчезването на редуващи се равнини.
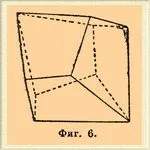
Останалите са холоедри. формите по този метод не променят външната си форма. Знакът на трапезоедъра е τ(hkl) и (mPn)/2.
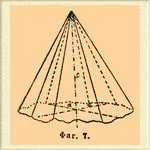
4)Хемиморфияна квадратна система. Една четворна ос на симетрия и четири равнини на симетрия. Хемиморфните форми могат да се получат от холоедричните, ако им позволим да се развият само в единия край на главната ос. По този начин от дитетрагонална бипирамида ще се получи проста дитетрагонална пирамида (фиг. 7); бипирамида от 1-ви и 2-ри вид ще даде съответните пирамиди; накрая, базопинакоидът ще даде само една равнина.
5)Хемиморфия на полустенаквадрат. системи. Само една четворна ос на симетрия.
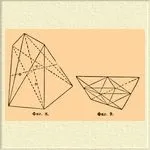
6)Скаленоеоричен хемиедър.Характеризира се с две взаимно перпендикулярни равнини на симетрия, пресичащи се в една оттрите двойниоси на симетрия, която (ос) също е четворна ос на сложна симетрия. Другите две двойни оси са перпендикулярни на първата и една на друга. Формите от този клас могат да се изведат от холоедричните, като накарат двойки равнини да изчезнат и да се развият (в диетарагонална бипирамида), отделни равнини (в тетрагонална бипирамида) и части от равнини (в други форми), лежащи в т.нар. октанти(пространства, ограничени от три взаимно пресичащи се равнини, в които лежат кристалните оси). Дитетрагонална бипирамида дава скаленоедър κ(hkl) и (mPn)/2 (фиг. 8); от тетрагонална бипирамида от 1-ви вид - квадрат. сфеноид κ(hhl) и (mP)/2.
От останалите форми нови не се получават.
7)Сфеноиден тетраедър.Една четворна ос на сложна симетрия и равнина на сложна симетрия, перпендикулярна на нея. Тук принадлежи квадратният сфеноид от 3-ти вид, който е напълно подобен на квадрата. сфеноид от 1-ви вид и се различава само по позицията си; неговите равнини са наклонени към кристалните оси под различни ъгли, както в осмоъгълна бипирамида, но броят на равнините тук е четири пъти по-малък.