Лабораторна работа по оптика - 31
Лаборатория #3
ИЗМЕРВАНЕ НА ФОКУСНО РАЗСТОЯНИЕ НА ТЪНКА ЛЕЩА
Въведение.Много оптични явления могат да се разглеждат въз основа на идеи за светлината като набор отсветлиннилъчи - линии, по които се разпространява светлинната енергия. В оптически хомогенна среда светлинните лъчи са праволинейни. На границата между две среди те се подчиняват на законите за отражение и пречупване. Светлинните лъчи могат да се пресичат без да се намесват и да се разпространяват след пресичане независимо един от друг. Разделът от оптиката, основан на тези концепции, се наричагеометричнаилилъчеваоптика. Една от основните задачи на геометричната оптика е изчисляването на пътя на лъчите в оптичните устройства, предназначени за получаване на изображения.
Пречупване на лъчи от сферична повърхност.Всяко оптично устройство е комбинация от отразяващи и пречупващи повърхности, които разделят оптически хомогенни среди една от друга. Обикновено тези повърхности са сферични или плоски. Равнината обаче винаги може да бъде представена като сферична повърхност с безкрайно голям радиус на кривина. Следователно сферичните повърхности са най-простите елементи, от които е изградена всяка оптична система.
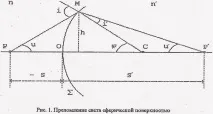
Да разгледаме сферична повърхностΣс център в точкаC, разделяща две прозрачни среди с показатели на пречупванеnиn'(фиг.1). Приемете за определеност, чеn'>nи светлината ще се счита за монохроматична, така че зависимостта наnиn'от дължината на вълната (дисперсия) не е значима. Може да се приеме (макар и не непременно), че пречупващата повърхност е ротационно симетрична по отношение на един от OCs, преминаващ през центъра на кривината. Такиваправата линия се наричаглавна оптична ос.
Нека точковият източникPе на главната оптична ос на системата. Нека вземем някакъв лъч от този лъч, напримерPM, падащ върхуΣпод ъгълi, да построим пречупен лъчMP'(ъгъл на пречупванеi') и да намерим позицията на точката, където пречупеният лъч пресича оста на системата. По-нататък всички сегменти по оста ще бъдат преброени от точкатаO(точката на пресичане на повърхносттаΣс остаPC), като сегментите, нанесени отO надясно(в посоката на разпространение на светлината), са положителни, а сегментите, нанесениналяво(срещу посоката на разпространение на светлината). Координатите на точкитеP,P'иCще бъдат означени съответно сS,S'иr. Така,PO = -S,OP' = +S',OC = +r.
O
Законът за пречупване в параксиалното приближение може да бъде написан като
. (1)
Ъгълътiе външният ъгъл на триъгълника ΔPMC, а ъгълътφе външният ъгъл ΔP'MC, следователно
,
.
Означаваме катоh— разстоянието от точкатаMдо остаPC, тогава за малки ъгли имаме
;
;
.
Тук се взема предвид, че при малки ъглиPM≈PO = -S,MP'≈ OP' = S',OC = MP' = r(радиус на сферата). Заместване в (1) на израза за ъглитеiиi'и заместване на ъглитеu,u',φс техните изрази(3), стигаме до отношението на Абе:
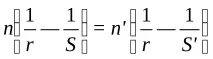
което е удобно за придаване на формата
.
Стойността от дясната страна на израз (5) зависи само от показателите на пречупване на разглежданите вещества и радиуса на кривината на повърхностите, които ги разделят. Следователно за дадени вещества и дадена повърхност тази стойност е постоянна; нарича сеоптична силана пречупващата повърхностФ:
.
Фактът, че формула (5) не включва ъгли, ни позволява да направим много важно заключение, че не само лъчътPM, но и всички други параксиални лъчи, излизащи от точкатаPна оптичната ос, след пречупване от сферичната повърхност, ще се пресичат приблизително в същата точкаP', която също лежи на оптичната ос. Следователно точкатаP'ще бъдеоптичното изображениена точкатаPв параксиалните лъчи. Две точкиPиP', които отговарят на условието, че ако едната от тях е обект, а другата е изображение, се наричат конюгирани.
Уравнение (5) обхваща всички случаи на пречупване на лъчи от сферична повърхност, като трябва да се помни, чеS,S'иrне са просто дължини на сегменти, акоординати на точки със знак. Използвайки правилото на знаците, можем да анализираме случая на изпъкнала (r > 0) или вдлъбната (r 0) точка, наречена изображение, наистина е точка на пресичане на пречупени лъчи. Такова изображение се наричареално. Във втория случай (S'0, тогава лещата се наричаположителна(колективна). АкоФ 1), намалена (β0) или обърната (β0) във въздуха (), формула (7), като се вземат предвид (8) и (9), може да бъде пренаписана като
,
къдетоa=OB,b=OEе разстоянието от лещата до обекта и отлещи преди изображението, респ. Оттук
Метод 2.Нека размерът на обектаlи размерът на изображението муl'. Тъй катоl/l' = a/b, формулата на Гаус (12) може да се трансформира в
.
Стойноститеb,lиl'се измерват експериментално и е препоръчително да се работи при големи увеличения.
Метод 3 (метод на Бесел).Ако разстоянието между обекта и екрана е не по-малко от 4f, тогава има две позиции на лещата, при които се получава рязко изображение на обекта (фиг.6). Едно от тези изображения е увеличено, а другото е намалено.
Нека обективът даде увеличено изображение в първата позиция, след товаb > а. Във втората позиция ще се получи намалено изображение, катоaиbса разменени (това може да се разбере, ако използвате обратни лъчеви пътища или съображения за симетрия). Обозначете
Очевидноzе разстоянието от обекта до екрана;xе разстоянието между две позиции на обектива, при които се получава рязко изображение. Нека изразимaиbчрезzиxи заместваме във формулата на Гаус (12):
.
Тази формула може да се използва и за определяне на фокусното разстояние на събирателна леща.