Лабораторна работа "Законите на Кеплер и конфигурацията на звездите", Платформа за съдържание

"Законите на Кеплер и конфигурацията на звездите"

Целта на работата:Изследването на моделите в движението на планетите и изчисляването на техните конфигурации.

Наръчници:Астрономически календар - постоянна част или справочник за любители астрономи, Астрономически календар - годишник на VAGO, таблици на логаритми, калкулатор, мобилна карта на звездното небе.

Теоретична справка:

Движението на планетите около Слънцето се описва от законите на Кеплер. Стойността на голямата полуос "а" на орбитата на планетата е средното разстояние на планетата от Слънцето. Поради незначителните ексцентричности "e" и наклони "i" на орбитите на големите планети, при решаване на задачи тези орбити могат да се считат за кръгови, с радиус "a" и лежащи практически в една и съща равнина - в равнината на еклиптиката. Изключение правят орбитите на планетите Меркурий и Плутон, но това предположение често важи и за тях.

Ъгловата и линейната скорост на планетата в орбита се променят периодично в съответствие със закона на Кеплер II и техните средни стойности могат да бъдат изчислени от средното разстояние "а" на планетата от Слънцето. Наистина, средната дневна ъглова скорост на планетата, наречена средно ъглово движение на планетата,

където T–е звездният период на въртене на планетата около Слънцето, изразен в средни дни.

Ясно за Земята

освен това във формула (3) T0 и T могат да бъдат изразени или в дни, или в години, но задължително в единици време.

Замествайки във формула (3) съотношението Т0 / Т, получено от третия закон на Кеплер, получаваме ώ като функция на средното разстояние “a” на планетата от Слънцето.

Сравняване на линейната скорост на планетата в орбита

със средна скоростЗемята

използвайки третия закон на Кеплер, намираме зависимостта υa от „a“.

формулите за ώ и υa са значително опростени, ако „a” се изрази в астрономически единици (AU) и се вземе за Земята ώ0=10 и υа=30km/s.

СидеричнитеTи синодичнитеSпериоди на революцията на планетата са свързани помежду си чрез контрола на синодичното движение и е най-лесно да се изчислят тези периоди в години, като се приеме за Земята нейният сидеричен период на революция 1 (една година). Ако е необходимо, намерената стойностSиTвинаги може да бъде изразена в дни. По подобен начин третият закон на Кеплер приема най-простата си форма, когатоTсе изразява в години и "a" в a. д.

Относителното положение на планетите се установява лесно по техните хелиоцентрични еклиптични сферични координати, чиито стойности за различни дни от годината се публикуват в астрономически календари - годишници, в таблица, наречена "хелиоцентрични дължини на планетите". Центърът на тази система е центърът на Слънцето (фиг. 1), а главният кръг е еклиптиката, чиито полюси P и P / са на разстояние 900 от нея.

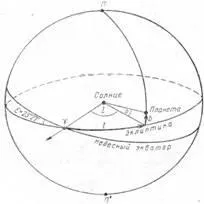
Големите кръгове, начертани през полюсите на еклиптиката, се наричат ​​кръгове на ширината и се използват за измерване на хелиоцентричната ширина "при" по протежение на еклиптиката, която се счита за положителна в северното еклиптично полукълбо на небесната сфера. Хелиоцентричната дължина „ℓ“ се измерва по протежение на еклиптиката от точката на пролетното равноденствие γ обратно на часовниковата стрелка до основата на кръга на ширината на звездата и има стойност, варираща от 01.01.01.

Поради малкия наклон на орбитите на големите планети спрямо равнината на еклиптиката (с изключение на орбитата на Плутон), тези планети винаги са разположени близо до еклиптиката и като първо приближение може да се счита тяхната хелиоцентрична ширина „при“ ≈ 00, определяща позицията на планетата спрямо Слънцетосамо нейната хелиоцентрична дължина „ℓ“. В този случай разположението на планетите спрямо Слънцето е изобразено на чертежа, чиято равнина е взета за равнината на еклиптиката (фиг. 2) и на която една от посоките е взета като посока към пролетното равноденствие γ. Фиг.2

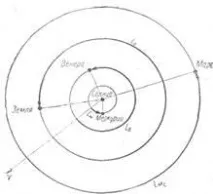
Ако е даден ден от годината, в който хелиоцентричната дължина на Земята ℓ0 има определена стойност, тогава на чертежа първо трябва да се отбележи местоположението на Земята, а след това върху него да се нанесат позициите на планетите или според тяхната известна хелиоцентрична дължина ℓ, или според зададени конфигурации. Хелиоцентричната дължина на Земята ℓ0 в определени дни от годината може да се намери и от геоцентричната дължина на Слънцето λ☼ в тези дни, така че ако изградите подобна система от еклиптични координати с началото в центъра на Земята, тогава винаги

защото Слънцето и Земята винаги са в противоположните краища на един и същи радиус-вектор (фиг.3). Но геоцентричната дължина λ на планетата не е свързана по подобен начин с нейната хелиоцентрична дължина 1, което лесно се вижда от чертежа (виж Фиг. 3) и равенството

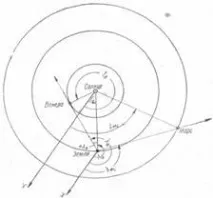
валидни само за определени конфигурации на планетите.

След като изградим позициите на планетите спрямо Слънцето от хелиоцентричните дължини, е възможно да измерим техните геоцентрични дължини λ с транспортир и по разликата

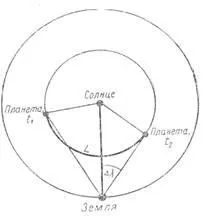
∆λ = λ – λ0 (6) Фиг.3

да се определят условията на тяхната видимост от Земята, като се приеме, че средно една планета става видима под ъгъл от около 150 от Слънцето.В действителност условията на видимост на планетите зависят не само от тяхното разстояние ∆λ от Слънцето, но и от тяхната деклинация 6 и от географската ширина на мястото на наблюдение, което влияе върху продължителността на здрача и височината на планетите над хоризонта.

Тъй като позицията на Слънцето върху еклиптиката е добре известна на всичкиден, тогава с помощта на звездната карта и стойностите на ∆λ е лесно да се посочи съзвездието, в което се намира планетата в същия ден от годината. Решаването на този проблем се улеснява от факта, че в долния край на картите на Малкия звезден атлас датите са отбелязани с червени цифри, на които кръговете на деклинацията, отбелязани с тях, кулминират в полунощ. Същите дати показват приблизителното положение на Земята в нейната орбита, наблюдавано от Слънцето. Следователно, след като се определят на картата екваториалните координати α0 и 60 на точката на еклиптиката, кулминираща в полунощ на дадена дата, е лесно да се намерят екваториалните координати на Слънцето за същата дата

α☼ = α0 + 12h и b☼ = - b0 (7)

и ги използвайте, за да покажете позицията си върху еклиптиката.

От хелиоцентричната дължина на планетите е лесно да се изчислят дните (датите) на началото на различните им конфигурации. Нека в някой ден от годината t1, хелиоцентричната дължина на горната планета е ℓ1, а хелиоцентричната дължина

на Земята е ℓ01 (фиг.4). Горната планета се движи по-бавно от Земята(ώ

---