Лекция № 2 “Пропозиционална логика”
Обща характеристика на твърдението.
Логически съюзи, техните таблични определения.
Първоначални типове пропозиционални логически символи.
Концепцията за пропозиционална логическа формула.
Таблични дефиниции на логическата стойност на формулата.
Понятието еквивалентна формула, видове формули на пропозиционалната логика.
Свойства на логически операции с оператори.
Пропозиционалната логика(илипропозиционалната логикаот английскиpropositionallogic) е формална теория, чийто основен обект е концепцията за логическо твърдение. По изразителност може да се характеризира като класическа логика от нулев ред. Пропозиционалната логика е най-простата логика, възможно най-близка до човешката логика на неформалното разсъждение и е позната от древността.
Предложение е всяка мисъл, която е представена под формата на декларативно изречение и за която може да се каже, че е вярна или невярна, но не и двете.
Твърденията включват езикови изрази като: „Небето е синьо“, „Математиката е най-интересната наука“, „Александър Македонски е учил при Аристотел“, „Добре е, когато човек спазва обещанията си“, „Назначавам те за лидер“ и др.
Изречението е граматически правилно изречение. Понятието граматически правилно изречение не се определя от логиката, то е взето от граматиката.
Съждението се изразява и съобщава чрез декларативно изречение. Въпросителното изречение не съобщава директно никаква информация; напротив, то съдържа искане за предоставяне на определена информация. Не може да се каже, че въпросителното изречение изразява преценка. Такова предложение изрично и директно не посочва нищо ине отрича нищо. Не съдържа послание, а само изразява въпрос.
Тези мотивационни изречения също не изразяват съждения, които са неволна, може да се каже, инстинктивна реакция на неочаквано разкрити обстоятелства: „О! - при болка "Ах!" - изненадано "Ех!" - при разочарование и др.
Одобрението е близко до преценката, но преценката е лишена от онази психологическа конотация, която винаги се свързва с акта на утвърждаване. Въпреки че предложението намира своя израз само в езика, то, за разлика от изречението, не зависи от конкретен език. Съобщението, че определена преценка е била изразена в определена ситуация, не е необходимо да посочва какъв език е бил използван в този случай. Ако някой каже: "Той ме увери, че ще се срещнем", няма въпрос на какъв език - български или испански - е дадено обещанието за среща. Едно и също предложение може да бъде изразено чрез различни изречения на един и същи език или различни езици. По този начин фразата „Римският писател Плавт каза, че човекът е вълк за човека“ казва каква преценка или каква мисъл е изразил Плавт, но не казва нищо за това какъв език е използвал в този случай. Ако кажем, че дадено изречение е изразено от някого, няма да можем да предадем мисълта си, докато не посочим какъв език е използван. Вярно е, че Плавт е заявил на латински твърдението „Homo homini lupus est“. Но не е вярно, че някога е казал на български изречението „Човек за човека е вълк“. По времето на Плавт български език още не е съществувал, нито Плавт, нито някой друг тогава е могъл да направи това твърдение.
Следователно предложението може да се характеризира като това, което две изречения имат общо, които са правилен превод едно на друго. Отзаддве различни изречения, български и английски: "Тази маса е кръгла" и "Тази маса е кръгла" означават едно и също предложение.
Изказването е единство от съждение и изречение.
Описателно изявление. Твърденията се делят на описателни (дескриптивни) и оценъчни.
Основните понятия на пропозиционалната логика сапропозиционална променлива— променлива, чиято стойност може да бъде логическо предложение — и(пропозиционална) формула, дефинирана индуктивно, както следва:
Акоpе пропозиционална променлива, тогаваpе формула.
Акоpе формула, тогава
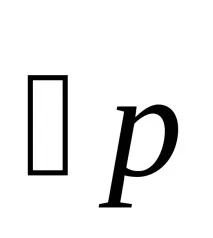
Акоpиqса формули, тогава те са формули.
Нищо друго не е формула.
Знаците
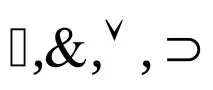
Подформулае част от формула, която сама по себе си е формула.Правилната подформулае подформула, която не отговаря на цялата формула.