Лекция 5
ОСНОВИ НА ТЕХНОЛОГИЯТА НА КВАЛИМЕТРИЯТА19
Идентифициране на оценени индикатори19
Правила за изграждане на дърво на свойствата21
Избиране на индикатор за всеки имот в последното ниво25
Определяне на тегловни коефициентиГрешка: Референтният източник не е намерен
Идентифициране на оценяваните индикатори
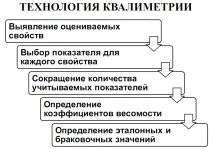
За да идентифицирате прогнозните показатели, трябва да знаете:
- как да се изгради дърво от свойства, които характеризират качеството (или интегралното качество) на даден обект;
- как да намерите съответния индикатор за всеки обект, тъй като за някои свойства на индикатори може да са необходими два или повече индикатора и трябва да изберете най-подходящия от тях.
Нови условия за този раздел:
Свойствата Equisatis (достатъчно равно, equus - равно, satis - достатъчно) са свойства, които са еквивалентни по отношение на влиянието си върху задоволяването на определена потребност, еднакво задоволяват тази потребност (задоволяват тази потребност еднакво), т.е.
Група от свойствае набор от свойства, на които комплексното имущество на equisatis е директно подразделено.
Ширина на групатае броят на свойствата в групата.
Независимост по предпочитание– два свойства, които са независими в група, когато е невъзможно да се даде предимство на нито един. Да предположим, че две свойства A и B са включени в една и съща група свойства и естеството на тези свойства е такова, че взети сами по себе си (т.е. свойство A, без да се взема предвид свойство B и обратно) по-големите стойности на показателите на всяко свойствопо-ниските стойности са за предпочитане. Ще кажем, че свойство A е във връзка с независимост на предпочитанията със свойство B, ако по-голямата стойност на индикатор A винаги е за предпочитане пред по-малките стойности, независимо какви стойности може да приеме индикаторът на свойство B.
Тези две свойства, които характеризират помещенията, като естествена светлина и площ, са независими по отношение на предпочитанията. Всъщност, каквато и да е площта на стаята, винаги повече естествена светлина ще бъде за предпочитане пред по-малко.
Независимо свойствое свойство, което е част от група свойства, така че е с което и да е от тях във връзка на независимост на предпочитанията.
Зависимо свойствое свойство в група свойства, което не е във връзка на независимост на предпочитанията с поне едно от тях.
Квази-просто свойство(квази - предполагаемо, въображаемо) е свойство, което може да бъде разделено на група от еквизати свойства, но което не е необходимо да бъде подложено на такова разделение, тъй като е известна функционалната зависимост между Q индексите на комплекса и еквизатис свойствата с него, образуващи група от свойства.
Дърво на свойствае графично представяне на разклонена структура, състояща се от комплексни свойства и свързани групи свойства. Дървото показва връзката между сложно, квази-просто и просто
Коренът на дървотое индикаторът за качество, който е на най-ниското ниво, т.е. най-сложното свойство на едно дърво.
Дясно (отляво, отгоре, отдолу) дърво на свойствата– дърво със свойства, в което за всяко комплексно свойство, съответната група от по-малко сложни свойства е разположена в чертежа вдясно (вляво,горе, долу) от него.
Дървен ред– това са секциите с минимална дължина на дървото, затворени между вертикални ивици за дясно или ляво дърво, или хоризонтални ивици за горно или долностранно дърво, разделящи всички комплексни свойства. Нивата са кодирани с числата 0, 1, 2, 3, ..., m.
Височина на дървото– общият брой нива m в дървото на свойствата.
Пълно дърво– дърво от свойства, чийто корен е на нулево ниво, разклонено до k-то ниво ( k = 1, m − 1). В едно непълно дясно дърво, крайните му десни клони могат да бъдат формирани не само от прости и квази-прости свойства (както в пълно), но и от сложни свойства.
Скъсено дървое пълно или непълно дърво, от което, в съответствие със ситуацията на оценка, е възможно да се изключат едно или повече свойства (прости или сложни) и (или) групи от свойства.
Поддървое раздел, избран от дадено дърво със свойства, което само по себе си е дърво с корен, разположен на k-то ниво на това дърво.
Дърво в строга форма на граф– дърво на свойствата, изобразено по начина, по който е прието в теорията на графите (с върхове и ребра), фиг.1.
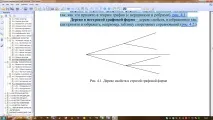
Дърво в нестрога графична форма– дърво от свойства, изобразено по начина, по който е обичайно да се изобразява например таблица със спортни състезания (фиг.2.)
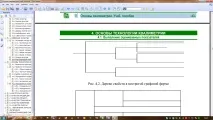
Дърво в таблична форма– дърво, изобразено под формата на класификационна таблица (фиг. 3).