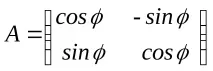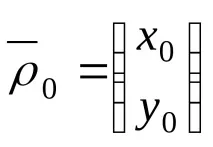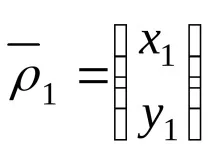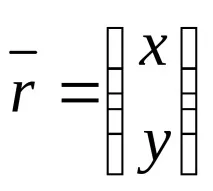Лекция 6

Равнинно движение на твърдо тяло

Равнинното движениена твърдо тяло е неговото движение, при което всяка негова точка се движи през цялото време в една и съща равнина.

Равнините, в които се движат отделните точки на тялото, са успоредни една на друга и успоредни на една и съща неподвижна равнина. Равнинното движение на твърдо тяло често се нарича плоскопаралелно. Траекториите на точките на тялото при равнинно движение са равнинни криви.

Равнинното движение на твърдо тяло е от голямо значение в инженерството. Въртеливото движение на твърдо тяло около неподвижна ос е частен случай на движението на твърдо тяло.

При изучаване на равнинното движение, както при всяко друго, е необходимо да се обмислят начини за уточняване на това движение, както и методи за изчисляване на скоростите и ускоренията на точките на тялото.

E

ако в тялото се начертае определена линия O1O2, перпендикулярна на равнините, в които се движат точките, тогава всички точки на тази линия ще се движат по една и съща траектория с еднакви скорости и ускорения; самата линия естествено ще запази ориентацията си в пространството. По този начин при плоско движение на твърдо тяло е достатъчно да се разгледа движението на една от секциите на тялото.

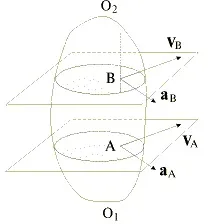
Сечението на твърдо тяло ще се нарича плоска фигура. Позицията на фигура в нейната равнина се определя изцяло от позицията на сегмент от права линия, здраво прикрепен към тази равнинна фигура.

Уравнения за равнинно движение на твърдо тяло

За да зададете позицията на равнинна фигура в равнината спрямо

координатната система, лежаща в равнината на фигурата, е достатъчно да зададете позицията на сегмента AB, прикрепен към фигурата в тази равнина.

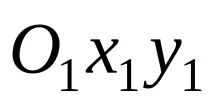
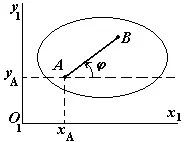
Позицията на отсечката AB спрямо координатната система

се определя чрез задаване на координатите на някоя точка от тазисегмент и неговата посока. Например, координатите на точка A () и посоката, зададена от ъгъла.

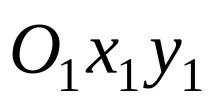
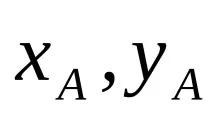
Уравненията на движение на плоска фигура спрямо координатната система

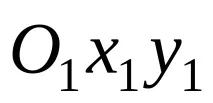
имат вида: .

Т

твърдо тяло с плоско движение има три степени на свобода.

се наричат ​​уравнения на равнинното движение на твърдо тяло.

P

Нека преминем към изследването на движението на една точка от твърдо тяло. Позицията на която и да е точка M от равнинна фигура спрямо подвижната референтна система,, прикрепена към тази движеща се фигура и лежаща в нейната равнина, се определя напълно чрез определяне на координатите x и y на точката M (фиг.6-3).

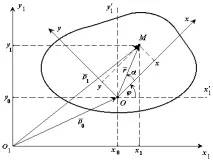
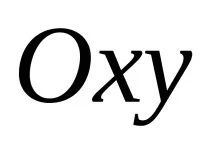
Съществува връзка между координатите на точка М в различни референтни системи:

, (6-1)

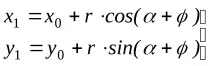
където

е дължината на сегмента OM,е постоянният ъгъл между OM и оста. Като вземем предвид изразите и получаваме

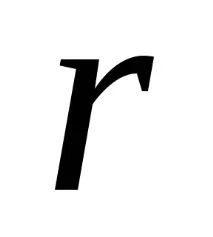
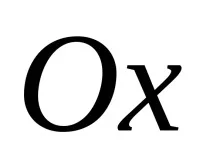
, (6-2)

Формули (6-2) са уравненията на движението на точка М на плоска фигура спрямо координатите

. Тези формули позволяват да се определят координатите на всяка точка от плоска фигура според дадените уравнения на движение на тази фигура и координатите на тази точка спрямо подвижна референтна система, прикрепена към движещата се фигура.

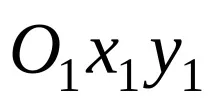
Използвайки матрично-векторна нотация, уравненията (6-2) могат да бъдат записани в следната форма:

, (6-3)

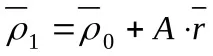
където A е матрицата на въртене в равнината:

,,,.

---