Локален и глобален минимум

Конспект на лекцията

1. Математическа постановка на задачата за оптимизация

2. Унимодален и мултимодален критерий 3. Локален и глобален минимум

4. Изпъкнал набор от допустими стойности на вектора на променливите параметри

5. Конвексен критерий за оптималност

6. Условия за съществуване на минимум в задачите за безусловна оптимизация

6.1. Едномерен оптимизационен проблем

6.2. Проблем с многовариантна неограничена оптимизация

7. Условия за съществуване на минимум в задачите за условна оптимизация

7.1. Задача за условна оптимизация с ограничения от тип равенство Функция на Лагранж

7.1.1. Теорема на Лагранж за оптимизационен проблем с ограничения от тип равенство

7.2. Задача за условна оптимизация с ограничения на неравенството

7.2.1. Концепциите за активни и неактивни ограничения

7.2.2. Теоремата на Кун-Тъкър за проблем с условна оптимизация с ограничения от неравенства

7.3. Задача за условна оптимизация с ограничения за равенства и неравенства

7.3.1. Теоремата на Кун-Тъкър за общ проблем за условна оптимизация с ограничения от тип равенство и неравенство

8. Класификация на оптимизационните проблеми

9. Примери за решаване на задачата за оптимизация

9.1. Проблем с оптималния дизайн на резервоара

9.2. Задачи за минимизиране на функция, дадена в аналитична форма

Въпроси за самопроверка към лекция 2

Математическа формулировка на задачата за оптимизация

, (1)

(2)

(3)

където е критерият за оптималност (скалар);

е векторът на променливите параметри;

Забележи, че

Задачата за намиране наминимум илимаксимум на критерия за оптималност (функция на целта) се наричазадача за оптимизация, с други думизадача за търсенеекстремум.

Проблем (1), (2), (3) -е проблем за условна оптимизация.

Ако ограниченията (2), (3) отсъстват, тогава това енеограничен оптимизационен проблем.

Унимодални и мултимодални критерии

Едномерен случай на унимодална функция (n=1).

Критерият за оптималност, където , се наричаунимодален критерий за оптималност, ако съществува такава точка, че функцията намалява на полуинтервала и нараства на полуинтервала.

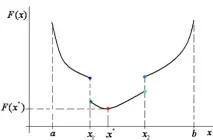
Двуизмерен случай на унимодална функция (n=2)

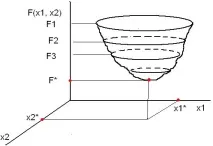
Критерият за оптималност, който има няколко локални минимума в областта на дефиниране, се наричамултимодален критерий за оптималност илимултиекстремален критерий за оптималност.

Едномерен случай на мултимодална функция (n=1)

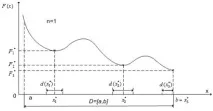
Местен и глобален минимум

Локален минимум в точка

е някакъв малък квартал на точката

Глобален минимум в точка

Къде е обхватът на приемливите стойности.

Точката на най-малкия от всички локални минимуми се наричаглобален минимум на функцията. Съответната стойност на функцията се наричаглобален минимум на тази функция

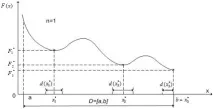
На фигурата за едномерния случай: - точки на локалния минимум на функцията , - съответните локални минимуми на тази функция, - точката на глобалния минимум и - глобалния минимум на тази функция.

---