Математически криви от втори ред, Анотация

Категория: Математика
Тип: Резюме

1. Криви от втори ред

2. Теореми, свързани с криви от втори ред

Криви от втори ред са изследвани за първи път от един от учениците на Платон. Неговата работа беше следната: ако вземете две пресичащи се прави и ги завъртите около ъглополовящата на образувания от тях ъгъл, получавате конична повърхност. Ако обаче тази повърхност се пресече с равнина, тогава в сечението се получават различни геометрични фигури, а именно елипса, кръг, парабола, хипербола и няколко изродени фигури.

Това научно познание обаче намери приложение едва през 17-ти век, когато стана известно, че планетите се движат по елиптични траектории, а оръдието лети по параболична. Дори по-късно стана известно, че ако дадете на тялото първата космическа скорост, то ще се движи в кръг около Земята, с увеличаване на тази скорост ще се движи по елипса, а когато се достигне втората космическа скорост, тялото ще напусне гравитационното поле на Земята в парабола.

1. Криви от втори ред

Крива от 2-ри ред е права в равнина, която в някаква декартова координатна система се определя от уравнението

ax2 + 2bxy + cy2 + 2dx + 2ey + f = 0

където a, b, c, d, e, f са реални коефициенти и a2 + b2 + c2 ≠ 0 .

Формата на кривата зависи от четири инварианти:

инварианти при въртене и изместване на координатната система:

инвариантен по отношение на въртенето на координатната система (полуинвариантен):

Много важни свойства на кривите от втори ред могат да бъдат изследвани с помощта на характерната квадратна форма, съответстваща на уравнението на кривата:

Така, например, една неизродена крива се оказва реална въображаема елипсаелипса, хипербола или парабола, в зависимост от това дали е положително определена, отрицателно определена, неопределена или полуопределена квадратна форма, която се установява от корените на характеристичното уравнение:

Корените на това уравнение са собствени стойности на реална симетрична матрица и, като следствие, винаги са реални:

Кривите от втори ред се класифицират на неизродени криви и изродени.

Доказано е, че кривата от 2-ри ред, определена от това уравнение, принадлежи към един от следните типове: елипса, хипербола, парабола, двойка прави (пресичащи се, успоредни или съвпадащи), точка, празно множество.

С други думи, за всяка крива от 2-ри ред (за всяко уравнение) има такава координатна система, в която уравнението на кривата има формата:

Елипса е геометричното място на точки в равнина, за което сумата от разстоянията до две фиксирани точки в равнината, наречени фокуси на елипсата, е константа. Отсечките, свързващи точката на елипсата с фокусите, се наричат фокални радиуси на точката.

Ако елипсата е описана от каноничното уравнение

където a > 0, b > 0, a> b > 0 са голямата и малката полуос на елипсата, тогава фокусите на елипсата са разположени симетрично по оста x и имат координати (−c, 0) и ( c, 0), където

Стойността e = c/a се нарича ексцентричност на елипсата.

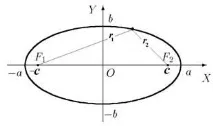
По дефиниция на елипса, r1 + r2 = 2a, r1 и r2 са фокусните радиуси, техните дължини се изчисляват по формулите

Ако фокусите на елипсата са еднакви, тогава елипсата е кръг.

Хипербола е крива от втори ред, която в някаква декартова координатна система се описва от уравнението

където a > 0, b > 0 - параметрихипербола.

Това уравнение се нарича канонично уравнение на хиперболата, а координатната система, в която хиперболата се описва от каноничното уравнение, се нарича канонична.

В каноничната система координатните оси са осите на симетрия на хиперболата, а началото на координатите е нейният център на симетрия.

Точките на пресичане на хиперболата с оста OX ( ± a, 0) се наричат върхове на хиперболата.

Хиперболата не се пресича с оста OY.

Отсечките a и b се наричат полуоси на хиперболата.

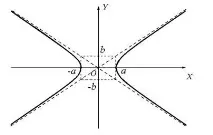
Правите линии ay − bx = 0 и ay + bx = 0 са асимптотите на хиперболата; тъй като точката на хиперболата отива към безкрайност, съответният клон на хиперболата се доближава до една от асимптотите.

Уравнението описва хипербола, чиито върхове лежат на оста OY в точките (0, ± b).

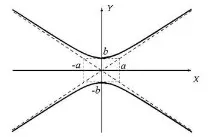
Такава хипербола се нарича нейните асимптоти, спрегнати на хиперболата - тези прави ay − bx = 0 и ay + bx = 0. Говори се за двойка спрегнати хиперболи.

Парабола е крива от втори ред, която в някаква декартова координатна система се описва от уравнението

където p > 0 е параболичният параметър.

Такова уравнение се нарича канонично уравнение на параболата, а координатната система, в която параболата се описва от каноничното уравнение, се нарича канонична.

В каноничната система абсцисната ос е оста на симетрия на параболата, а началото е нейният връх.

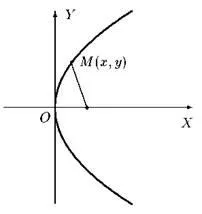
Уравненията y2 = −2 px, x2 = 2 py и x2 = −2 py, p > 0, в същата канонична координатна система също описват параболи:

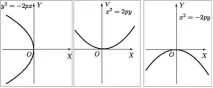
2. Теореми, свързани с криви от втори ред

Теоремата на Pascaml е теорема в проективната геометрия, която гласи, че:

Ако шестоъгълник е вписан в кръг или друго конично сечение (елипса, парабола, хипербола,дори двойка прави линии), тогава точките на пресичане на три двойки противоположни страни лежат на една и съща права линия. Теоремата на Паскал е двойствена на теоремата на Брианшон.

Теоремата на Брианшон е класическа теорема на проективната геометрия. Тя ще бъде формулирана по следния начин:

Ако шестоъгълник е описан около конично сечение, тогава три диагонала, свързващи противоположни върхове на този шестоъгълник, минават през една точка.

По-специално, в изроден случай:

Ако страните на шестоъгълник минават последователно през две дадени точки, то трите диагонала, свързващи срещуположните му върхове, минават през една точка.

Теоремата на Брианшон е двойствена на теоремата на Паскал, а нейният изроден случай е двойствен на теоремата на Папус.

1. Корн Г., Корн Т. Криви от втори ред (конични сечения) // Наръчник по математика. - 4-то издание. - М: Наука, 1978. - С. 64-69.

2. Корн Г., Корн Т. 2.4-5. Характеристична квадратна форма и характеристично уравнение // Наръчник по математика. - 4-то издание. - М: Наука, 1978. - С. 64.

3. В.А. Илин, Е.Г. Позняк. Аналитична геометрия, гл. 6. М.: "Наука", 1988 г.