Математиката в древен Египет е

Статията е посветена на състоянието и развитието наматематиката в Древен Египетв периода приблизително от 30-ти до 3-ти век пр.н.е. д.

Най-старите древноегипетски текстове по математика датират от началото на 2-ро хилядолетие пр.н.е. д. След това математиката се използва в астрономията, навигацията, геодезията, при изграждането на сгради, язовири, канали и военни укрепления. В Египет не е имало парични разплащания, като самите пари. Египтяните са писали на папирус, който е зле запазен и следователно познанията ни за математиката на Египет са значително по-малко от тези на математиката на Вавилон или Гърция. Вероятно е бил по-добре развит, отколкото може да се предположи от достигналите до нас документи - известно е [1], че гръцките математици са учили с египтяните [2] .

Не знаем нищо за развитието на математическите знания в Египет, нито в по-древни, нито в по-късни времена. След възцаряването на Птолемеите започва изключително плодотворен синтез на египетската и гръцката култури.

Съдържание

Основните оцелели източници датират от периода на Средното царство, разцвета на древноегипетската култура:

Папирусът на Амес или Папирусът на Ринда е най-обемистият ръкопис, съдържащ 84 математически задачи. Написана около 1650 г. пр.н.е. д.
Московски математически папирус (25 задачи), около 1850 г. пр.н.е д., 544 × 8 см.
Така нареченият "кожен свитък", 25 × 43 см.
Папируси от Лахуна (Кахуна), съдържащи редица фрагменти на математически теми.
Берлински папирус, около 1300 г. пр.н.е. д.
Кайро дървени таблетки (таблетки Akhmim).
Папирус Райзнер, около 19 век пр.н.е. д.

Няколко фрагмента с изчислителен характер са достигнали до нас от Новото царство.

Авторите на всички тези текстове са ни неизвестни. Копията, които са достигнали до нас, са предимно копия, копирани през периода на Хиксос. Носителите на научно знание тогава се наричат писарии всъщност са държавни или храмови служители.

Всички задачи от папируса на Ахмес (записан ок. 1650 г. пр. н. е.) имат приложен характер и са свързани с практиката на строителството, определяне на границите на парцели и др. Задачите са групирани не по методи, а по предмет. В по-голямата си част това са задачи за намиране на площите на триъгълник, четириъгълници и кръг, различни операции с цели числа и аликвотни дроби, пропорционално деление, намиране на съотношения, повдигане на различни степени, определяне на средно аритметично, аритметични прогресии, решаване на уравнения от първа и втора степен с едно неизвестно [3] .

Няма абсолютно никакви обяснения и доказателства. Желаният резултат се дава директно или се дава кратък алгоритъм за неговото изчисляване.

Този метод на представяне, типичен за науката на страните от древния Изток, предполага, че математиката там се е развила чрез индуктивни обобщения и гениални предположения, които не са формирали никаква обща теория. Въпреки това в папируса има редица доказателства, че математиката в древен Египет от онези години е имала или поне е започнала да придобива теоретичен характер. Така египетските математици знаеха как да извличат корени и да се издигат до степен, да решават уравнения, бяха запознати с аритметичната и геометричната прогресия и дори усвоиха основите на алгебрата: при решаването на уравнения специален йероглиф „куп“ обозначаваше неизвестното.

Номериране (писане на числа)

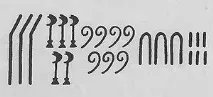
Древноегипетското номериране, тоест писането на числа, беше подобно на римското: отначало имаше отделниикони за 1, 10, 100, ... 10 000 000, комбинирани адитивно (сгъваеми). Египтяните са писали от дясно на ляво, като най-младите цифри на числото са записвани първи, така че в крайна сметка редът на числата съответства на нашия. В йератичната писменост вече има отделни символи за числата 1-9 и съкратени знаци за различните десетици, стотици и хиляди.

Всяко число в древен Египет може да бъде написано по два начина: думи и числа. Например, за да напишете числото 30, можете да използвате обикновени йероглифи: