Матрични уравнения

Разгледайте матрични уравнения от формата:

Теорема 4.4. (относно матричните уравнения).Матринно уравнение(1)когато A0има уникално решениеX=A–1B.

Матринното уравнение(2)при C0има уникално решение

Примери.1. Решете уравнението:AX=B, къдетоA=

,B=.

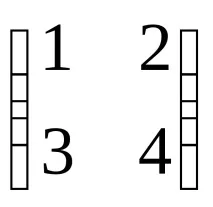
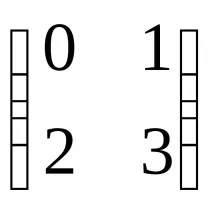
A0, така че решението на уравнението ще бъде матрицатаX=A–1B.ИзчислетеA–1с помощта на елементарни трансформации:

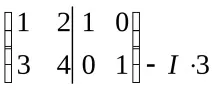
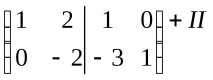
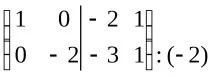
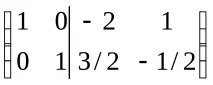
Следователно,A-1=

.X=·=.

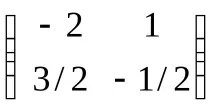
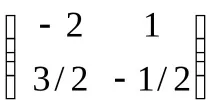
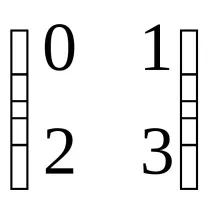
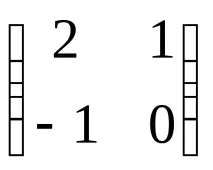
Проверка:

·=.

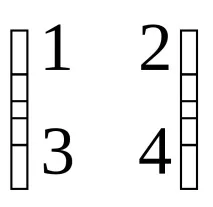
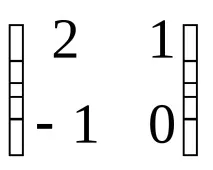
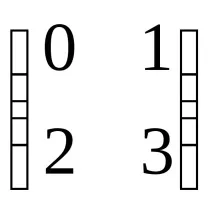
Отговор:X=

.

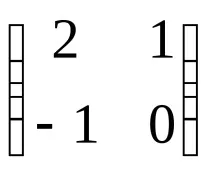
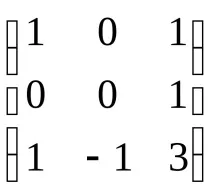
2. Решете уравнението:YC=D, къдетоС =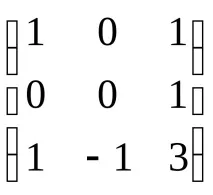

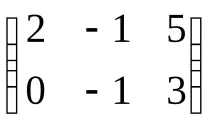
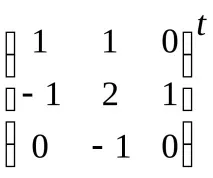
,D=

.

ИзчислетеС–1=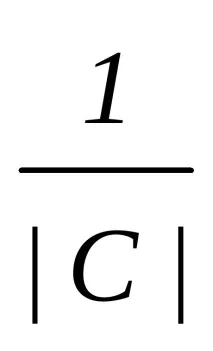

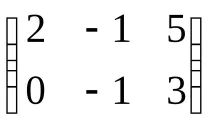
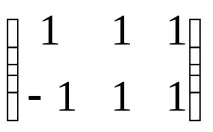
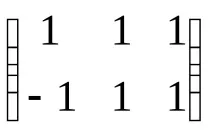
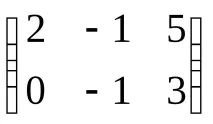
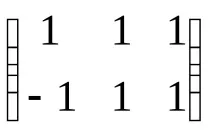
Сijt= 

=

,Y=DC– 1= =



=

.Тест:

=

.Отговор:Y=

.

МЕТОДИКА 14. Тема на урока: Решаване на системи от линейни уравнения

Цели на урока: запознаване с дефиницията на система от линейни уравнения; с дефиницията на решението на системата; с основните методи за решаване на системи от уравнения; развиване на умение за прилагане на аналогия при решаване на проблеми;

1. Организационен момент; 2. Повторение на вече изучен материал; 3. Изучаване на нова тема; 4. Домашна работа; 5. Обобщаване;

Фрагмент от урока: Поздрав към учениците.

Повторение на предварително изучен материал: (учениците сами определят кръга от въпроси, задават си един на друг)

Какво е уравнение? (Уравнението е равенство,съдържащ една или повече променливи) - линейно уравнение с 1 променлива.

Какво се нарича линейно уравнение с 2 променливи? ()

Дайте примери за линейни уравнения с 2 променливи.

Какво е решението на линейно уравнение с 2 променливи?

Задача 1: Разликата между две числа е 6. Намерете тези числа. (

)

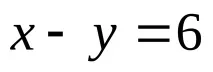
Какви свойства на уравненията знаете?

Свойства на уравненията: - ако в уравнението пренесем члена от една част в друга, като сменим знака му, то получаваме уравнение, еквивалентно на даденото;

ако двете страни на уравнението се умножат или разделят на едно и също ненулево число, тогава се получава уравнение, което е еквивалентно на даденото.

Задачи за усвояване на материала:

1. Решете системата от уравнения:

2. Начертайте линейното уравнение 3x - 2y = 6

3. Известно е, че графиката на функцията 2x + 3y = 2 минава през точка A, чиято ордината е 4. Намерете абсцисата на тази точка.

Билет номер 15. Билет номер 15. Полиноми в една променлива. Делимост на полином на бином Пръстенът f[X] от полиноми над поле

Дефиниция 5.1.Нека произволно полеF,x –е променлива.Полиномn-та степен на една променливае израз на формата:anxn+ …+ a1x + a0, къдетоai

F(i= 0, 1, 2, …,n),an0 ,nN.

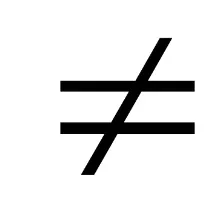
Забележка.aiхiсе нарича член на полинома;iе степента на този член (акоai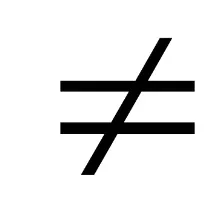

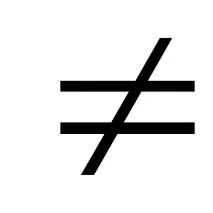
0);aiе коефициентът на съответния член. Акоai= 0, тогава наaixiне се присвоява никаква степен,a0x0–е член от нулева степен, акоai0 е елемент от полетоF.

Полиномите в една променлива се означават по следния начин:f(x),g(x),h(x) и т.н.

Дефиниция 5.2.Степента на полином f(x) е най-високата степен на неговите членове (и се обозначава сdegf(x)).

Полиномътf(x) = 0хn+ 0xn-1+ … + 0 се наричанулев многочлен. Степента му не е определена.

2) полиноми с нулева степен (ai

F);

3) полиноми със степен по-голяма от нулаf(x) иg(x), …

Ако са дадени два полиномаf(x) иg(x), тогава винаги можем да приемем, че те съдържат еднакъв брой членове, тъй като липсващите членове винаги могат да бъдат присвоени с нулеви коефициенти.

Дефиниция 5.3.

f(x),g(x)F[x] ако

f(x) =g(x)

(an=bn)(an-1=bn-1)…(a0=b0).

Нека дефинираме три операции върху множествотоF[x]:

1.

f(x),g(x)F[x],f(x) +g(x) = (an+bn)xn+(an-1+bn-1)xn-1+ …+(a1+b1)x+ +(a0+b0);

2.

f(x)F[x],

F,

f(x) =

anxn+

an-1xn-1+ … +

a1x +

a0;

3.

f(x),g(x)F[x],f(x)g(x) =a0b0+ (a0b1+a1b0)х+ …+ (a0bi+…+a1bi-1+ + … +aib0)xi+ … +anbm)xn+m;

Теорема 5.1 (за пръстена от полиноми на една променлива).

Алгебра(F[x], + , )е комутативен пръстен с единица без делители на нулата, съдържащ като подпръстен полетоF.

---