МЕТОДИ ЗА ПОЛУЧАВАНЕ НА ДИСКРЕТНИ АНАЛОЗИ
Изхвърляйки членовете на двете серии, започвайки от четвъртата, изваждайки и добавяйки уравненията, получаваме
Чрез заместване на тези изрази в диференциално уравнение може да се получи уравнение с крайна разлика.
Този метод предполага, че промяната в с е близка до полинома, така че по-високите производни могат да бъдат пренебрегнати. Това предположение обаче води до нежелани последствия, например за случая на експоненциална промяна. Извеждането с помощта на редовете на Тейлър е сравнително просто, но по-малко гъвкаво и не допринася за разбирането на физическото значение на членовете на уравнението.
Вариационен метод.Друг метод за получаване на дискретни аналози се основава на вариационното смятане.
В вариационното смятане се показва, че решението на тези диференциални уравнения е еквивалентно на минимизиране на съответната величина - функционала. Тази еквивалентност се нарича вариационен принцип. Желаният дискретен аналог се получава от условията за минимум на функционала по отношение на стойностите на зависимата променлива в възловите точки. Вариационният метод се използва много често в методите на крайните елементи за изследване на напреженията, където може да се свърже с принципа на виртуалните премествания. В допълнение към математическата сложност и трудността за разбиране, основният недостатък на метода е неговата ограничена приложимост, поради факта, че вариационният принцип не съществува за всички диференциални уравнения, които представляват интерес.
Метод на претеглените остатъци.Ефективен метод за решаване на диференциални уравнения е методът на претеглените остатъци. Основният подход е прост и интересен. Представяме диференциалното уравнение във формата
Да приемем, че приблизителното решение има например формата
където са неизвестни параметри. Заместник вдиференциално уравнение (2.6) и изберете несъответствието, което е равно на:
Искаме да направим този остатък малък в известен смисъл. Нека се преструваме, че
където е тегловната функция, а интегралът се взема за разглеждания регион. Чрез избиране на последователност от тегловни функции може да се получи достатъчен брой уравнения за намиране на параметрите. След като решим получената система от алгебрични уравнения за неизвестни параметри, намираме приблизително решение на диференциалното уравнение. Избирайки различни класове тегловни функции, можете да получите различни версии на метода (със собствени имена).
Този метод беше широко използван за решаване на уравнения на граничния слой, докато почти не беше заменен от метода на крайните разлики. Въпреки това, може да се установи връзката му с метода на крайните разлики, или по-точно с метода на дискретизация, ако разглеждаме приблизителното решение не като единична алгебрична функция за целия регион, а като профил на части с неизвестни параметри, които са стойности в възлови точки. Всъщност голяма част от скорошното развитие на метода на крайните елементи също се основава на използването на профили на части в комбинация с вариант на метода на претеглените остатъци, известен като метода на Галеркин.
Най-простата тегловна функция е . С помощта на такава функция, в рамките на този метод, е възможно да се изгради система от уравнения, като се раздели изчислителната област на поддомейни или контролни обеми и се изберат като тегловни функции, които едновременно са равни на единица в една от поддомейните и нула във всички останали. Този вариант на метода на претегления остатък се нарича метод на поддомейн или метод на контролния обем. Предполага се, че интегралът на остатъка върху всеки контролен обем трябва да бъде равен на нула.
Метод на обема на пробата.Често в началните учебници по пренос на топлина се дава извеждането на уравнение с крайна разлика с помощта на метода на серия Тейлър и след това се показва, че полученото уравнение съответства на условието на топлинния баланс в малка област, съдържаща възловата точка. Видяхме също, че методът на контролния обем може да се разглежда като специален случай на метода на претегления остатък. Основната идея на метода на контролния обем е лесно разбираема и се поддава на директна физическа интерпретация. Изчислителната област е разделена на редица непресичащи се контролни обеми по такъв начин, че всяка възлова точка се съдържа в един контролен обем. Диференциалното уравнение се интегрира върху всеки контролен обем. За изчисляване на интеграли се използват профили на части, които описват промяната между възловите точки. В резултат на това се намира дискретен аналог на диференциалното уравнение, който включва стойности в няколко възлови точки.
Дискретният аналог, получен по този начин, изразява закона за запазване за краен контролен обем по същия начин, по който диференциалното уравнение изразява закона за запазване за безкрайно малък контролен обем. Едно от важните свойства на метода на контролния обем е, че той съдържа точното интегрално запазване на такива величини като маса, импулс и енергия върху всяка група контролни обеми и, следователно, върху цялата изчислителна област. Това свойство се проявява за произволен брой възлови точки, а не само в пределния случай на много голям брой от тях. По този начин дори решението с груба мрежа удовлетворява точни интегрални баланси.
Резултатът от решаването на дискретни уравнения по отношение на стойностите в възловите точки може да се разглежда по два начина. В метода на крайните елементи и повечето претеглени методиостатъци, изчислената промяна се приема като приблизително решение, състоящо се от стойностите в възловите точки и интерполационните функции (или профили) между възловите точки. За разлика от това, при метода на крайните разлики само стойностите в възловите точки се считат за решение и не се правят изрични указания за естеството на промяната между тези точки. Тази ситуация напомня на лабораторен експеримент, при който разпределението на дадено количество е дадено като измерени стойности в някои дискретни точки и не е определено изменението му в интервалите между тези точки. Ние също използваме този подход в метода на контролния обем и ще търсим решение под формата на стойности само в възловите точки. Ще разглеждаме интерполационните формули или профили като спомагателни, необходими за изчисляване на интеграли. След получаване на дискретни аналози, предположенията за естеството на профилите могат да бъдат игнорирани. Тази гледна точка дава пълна свобода за използване на различни профили за интегриране на различни членове на диференциалното уравнение.
За по-голяма яснота прилагаме метода на контролния обем към прост проблем.
Нека разгледаме стационарен едномерен проблем с топлопроводимостта, описан от уравнението
където е коефициентът на топлопроводимост; - температура; е скоростта на отделяне на топлина за единица обем.
Подготовка.За получаване на дискретен аналог, показаната пара фиг. 2.2 местоположение на възловите точки.
Фиг. 2.2. Модел на гореща точка за 1D проблем
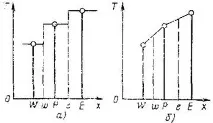
Ориз. 2.3. Прости приближения на профила:
а - стъпаловиден профил; b - частично линеен профил
Фокусът на нашето внимание е точката P, заобиколена от точки E и W (E е източната страна, т.е. посоката по оста; W е западната страна,т.е. посоката, обратна на посоката на оста). Прекъснатите линии показват границите на контролния обем; сега не се интересуваме от точното им местоположение. Тези граници са маркирани с e и w. За разглежданата едномерна задача приемаме, че размерите на контролния обем по направления и са равни на единица. По този начин обемът на показания контролен обем е . Интегрирайки (2.10) върху контролния обем, получаваме
Предположение за формата на профила.Нека сега направим предположение за формата на профила или формулата за интерполация. На фиг. 2.3 показва два прости профила. В най-простия случай се приема, че стойността в възловата точка се запазва за целия контролен обем около нея. Това предположение води до това, показано на фиг. 2.3, но към стъпаловиден профил. За такъв профил производната на границите на контролния обем (т.е. в точки w или e) не е дефинирана. Тази трудност не възниква за частично линеен профил (фиг. 2.3.6), при който промяната между възловите точки се описва с линейни интерполационни функции.
Дискретно аналогово.Използвайки частично линеен профил за определяне в уравнение (2.11), получаваме
където е средната стойност върху контролния обем. Полезно е да напишете уравнение (2.12) в следната форма: