Методи за решаване на транспортни проблеми
1) Избираме променливите на задачата x1 - произведения от видаA1; x2 - произведения от видаА2.
Съставяме система от ограничения под формата на неравенства
Съставете целевата функцияz(x)= 25 x1 + 17 x2 → max, т.е. осигуряване на максимални приходи от продажбата на готовата продукция.
2) Нека намерим решение на формулирания проблем, използвайки неговата геометрична интерпретация. Първо, дефинираме полигона на решението. За да направите това, в неравенствата на системата от ограничения и условията за неотрицателност на променливите заместваме знаците на неравенствата със знаците на точни равенства и намираме съответните прави линии
Тези линии са показани на фиг. 1. Пресечната точка на получените полуравнини определя многоъгълника на решенията на тази задача.
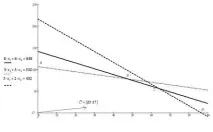
Ориз. 1. Графично представяне на математическия модел
Както се вижда от фиг. 1, многоъгълникът на решението е петоъгълникътOABSD. Координатите на всяка точка, принадлежаща на дадения петоъгълник, удовлетворяват дадената система от неравенства и условието за неотрицателност на променливите. Следователно формулираната задача ще бъде решена, ако се намери точка, принадлежаща на петоъгълникаОАВСD, където функциятаzприема максимална стойност. За да намерим определената точка, ние конструираме вектор
Преместване на тази линия по посока на вектора
Намерете координатите на точкатаCкато координати на пресечната точка на правите 8 x1 + 6 x2 = 848 и 5 x1 + 2 x2 = 432.
Решавайки тази система от уравнения, получаваме
3) Нека запишем тази задача под формата на основната задача на линейното програмиране. За да направим това, преминаваме от ограничения за неравенство към ограничения за равенство. Въвеждаме три допълнителни променливи, в резултат на което ограниченията се записват под формата на система от уравнения
Правим таблица на първата итерация:
В 4-ти ред на таблицата. в променливи колони
От табл. се вижда, че намереният нов основен план на първоначалната задача X* = (64;56; 0; 60; 0) е оптимален. В този случай maxz= 2552.
Така че приходите от продажби ще бъдат най-големи, ако производственият план включва пускането на 64 продуктаA1и 56 продуктаA2и е 2552 den. единици
4) За тази задача
Следователно, двойственият проблем е следният: намерете минимума на функциятаz*(x)= 848 y1 + 532 y2 + 432 y3 при условията
Последната симплексна таблица (итерация 3) показва товадвойният проблем има решение
1) Метод на разпространение
Нека вземем някои обозначения:i- индекс на редj- индекс на колонаm- брой доставчициn- брой потребителиXi,j- транспортиране между доставчикAiи потребителBj.