МЕТОДЪТ НА КАНТИРАНЕ е
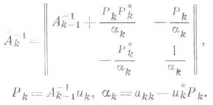
Изчислителната схема на О. м. за решаване на системата се състои в следното. Нека ,k=1,2. . . ., P;b(n,n+1) =-b.If е неособена матрица и е решение на системата
, тогава решението на системата се намира от представянето
и от (2), както следва:
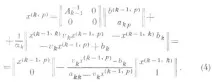
По този начин, от решения на и системи с една и съща матрица и различни десни части, е лесно да се получи решение на система с оградена матрица. Решение на оригиналната система: x (n,n+1) . Може да се получи чрез периодично прилагане на съотношението (4). Това се свежда до последователно изчисляване на набора от вектори,k=1,2,. . ., n,p>k, т.е.
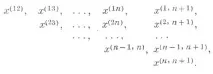
По отношение на количеството изчислителна работа горната схема на O. m. е еквивалентна наметода на Гаус,един от най-бързите директни методи за решаване на системи.
Om прави възможно решаването на системи от по-висок ред чрез ефективно използване на компютърната памет. Това се дължи на факта, че за да се изчислят векторите, p>k, се изисква да се запомнят само векторите, p>(k-1), и коефициентите на k-тото уравнение на системата, т.е. масив от числа с дължина f(k).= k(n-k+1).(n+1). Следователно, за да се реши система от n-ти ред, е достатъчно да има работно поле с дължина (n+1) (n+5)/4 (n/2) 2 . В този случай елементите на матрицата и дясната страна могат да бъдат въведени в паметта на компютъра не веднага, а последователно - ред по ред.
Целесъобразно е да се използва О. м. при решаване на система, за която вече е решена пресечена система. Тогава съотношението (4) веднага дава желаното решение.
Описаната схема на О. м. може да се използва за изчисляване на детерминантата. От представяне (1) следва, че
Прилагането на тази връзка рекурсивно даваA.
Също като обжалванетоматрици, решението на системата и изчисляването на детерминанта по отношение на молекулярни матрици е възможно само за матрици с ненулеви главни второстепенни. По принцип тук също е необходимо да се използва схемата за избор на основни елементи.
Спр.: [1] Воеводин В.В., Числени методи на алгебрата, М., 1966; [2] Фадеев Д.К., Фадеева В.Н., Изчислителни методи на линейната алгебра, 2-ро издание, М.-Л., 1963.
Математическа енциклопедия. — М.: Съветска енциклопедия. И. М. Виноградов. 1977-1985 г.