Модели на пълзене, базирани на теорията за стареенето
Най-простата теория за пълзенето е теорията за стареенето. Според тази теория трябва да има връзка
където е общата деформация и напрежение при просто опън, t и T са времето за натоварване и температурата. В съответствие с равенство (94), общата деформация
За сложно състояние на напрежение зависимостта (96) се отнася до интензитетите на деформациите и напреженията:
или под друга форма
Интензивността на общата деформация (еластичност, пластичност и пълзене) се определя от интензивността на напреженията, времето и температурата на натоварване.
За стационарен режим на натоварване ) зависимост
може да се определи от експеримент (криви на пълзене). Основната хипотеза на теорията за стареенето е, че зависимостта (99) е валидна за нестационарно натоварване
Изчислението на пълзене се основава на криви на пълзене (вижте раздел 15), начертани при постоянни температури за различни нива на напрежение. На фиг. 5.17 показва мрежа от криви на пълзене при напрежения
По абсцисната ос е нанесено времето, а по ординатната ос - деформацията при разтягане на пръта (пробата) при постоянно напрежение. В момента (референтна точка) първоначалната деформация съответства на моментната деформация (еластична или еластично-пластична) в резултат на приложеното напрежение.
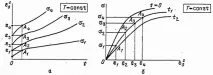
Ориз. 5.17. Конструиране на изохронни криви на пълзене (b) от мрежа от криви на пълзене (a)
при конструиране на криви на пълзене, както и криви на деформация, не се взема предвид.
Ако начертаете разрез , например , тогава правата линия ще пресича кривите на пълзене в точки , които съответстват на деформации на пълзене .
Във всяка точка е известна стойността на ефективното напрежение Тези данни ни позволяват да изградим зависимост
На фиг. 5.17 крива (101) преминава през точки Зависимост (101) изразява изохронна крива на пълзене за време t.
За началната стойност на времето t = 0, изохронната крива съвпада с обичайната крива на деформация на опън на пръта. Мрежата от криви на деформация може да бъде представена като повърхност на общите деформации на пълзене (фиг. 5.18) в координати
Равнините (защриховани на фиг. 5.18) образуват изохронни криви на пълзене при пресичане с повърхността.
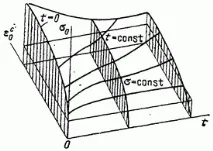
Ориз. 5.18. Повърхност на общите деформации при пълзене
Според теорията на стареенето, която е представена в интерпретацията на Ю. Н. Работнов, пълзенето води до намаляване на еластично-пластичното съпротивление на материалите - с увеличаване на времето условните криви на деформация намаляват, материалът "остарява".
Обърнете внимание, че деформации при пълзене възникват и при напрежения, по-ниски от границата на провлачване, и следователно се получава „намаляване“ и в еластичния участък на кривите на условната деформация.
След намиране на изохронните криви на пълзене, проблемът се свежда до изчисляване на еластично-пластично тяло според деформационната теория на пластичността (§ 19). За началния момент от време изчислението напълно съвпада с определянето на напреженията деформации съгласно деформационната теория на пластичността.
За време t се извършва точно същото изчисление, но като крива на деформация се приема изохронната крива на пълзене за съответното време.
Моделите на пълзене, базирани на теорията на стареенето, са подходящи за описание на монотонно или стационарно натоварване, процеси на релаксация (спад) на напрежението притрайна деформация.
Основният недостатък на теорията за стареене е отричането на влиянието на историята на натоварването. От уравнение (98) следва, че в момент t дадено напрежение съответства на определена деформация на пълзене. Следователно, ако напрежението моментално се увеличи, тогава деформацията на пълзене също трябва да се увеличи незабавно, което, разбира се, не може да се случи.
По-правилно е да се приеме, както се прави в други теории за пълзене, че при мигновено увеличаване на напреженията скоростта на пълзене нараства по подобен начин.