Напрегнато-деформирано състояние на гредата
Напрегнато-деформирано състояние на греда при пряко напречно огъване
1. В най-простия случай на директно огъване на гредата външните натоварвания действат в една (вертикална) равнина, перпендикулярна на оста на гредата.
2. Върху гредата могат да действат сили:
Б) разпределени по дължина (среща се по-често в строителството)
Б) огъващи моменти
Анализът навътрешнитесилови фактори започва с дефинирането на пълна система отвъншни сили.
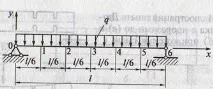
3. Разгледайте хоризонтална греда с правоъгълно напречно сечение върху две опори и натоварена с равномерно разпределено вертикално натоварване q.
4. Напречното сечение на гредата е с височина h
5. Ако гредата лежи свободно върху опорите, тогава една опора се счита за шарнирно фиксирана, другата - шарнирно подвижна. Такъв лъч се нарича прост.

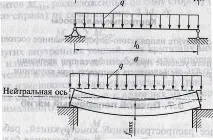
1. Ако преди натоварването гредата беше права лента, тогава под натоварване лентата се огъна и се появи завой:
A) от страната на товара прътът стана вдлъбнат (компресиран);
Б) от противоположната страна - изпъкнал (опънат)
2. Деформации (неравномерно разпределение)
А) при огъване надлъжните влакна се деформират по различен начин: някои се удължават в долната част на гредата, други се скъсяват в горната част на гредата;
Б) тези удължения и скъсявания са различни в зависимост от разположението на влакната спрямо средата на сечението: колкото по-близо до ръба, толкова по-голяма е деформацията.
В) неутралната ос (слой) не променя дължината си по време на кривината.Неутрална ос– разделя зоните на натиск и опън, променя позицията си с увеличаване на натоварването
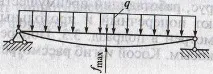
3. Отклоняване - преместване на точките на лъча надолу поради кривината на оста. Най-голямото отклонение е в средата на гредата
fmax = 5384∙ql4EJ
1. Във всеки участък по дължината на гредата има:
А) огъващи моменти Mx и
Б) напречни сили Qx
2. Стойността на Mx и Qx зависи от:
А) проектната схема на гредата;
Б) естеството на натоварването
3. Mx и Qx диаграми за обикновена греда от равномерно разпределен товар
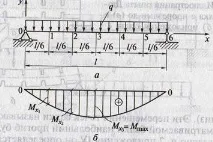
4. Най-високата стойност на Mx се определя по формулата
5. Най-високата стойност на Qx се определя по формулата
1. В съответствие с неравномерното разпределение на деформациите: напреженията по височината на сечението не са еднакви.
2. Най-голямото напрежение съответства на най-големите деформации (закон на Хук)
3. Крайните части на напречното сечение, най-отдалечените от средата по височината на сечението, са в напрегнато състояние.
4. Ето защо, когато се определят напреженията на огъване, е необходимо да се вземе предвид не самоброят на материалите (Sсечения), но иразпределението му по височината на сечението.
5. Най-изгодни при огъване са участъците, в които по-голямата част от материала е разположена в краищата на елемента.
6. Разпределение на напрежението
А) в крайните горни влакна се появяват най-големите напрежения на натиск σхсж. Условно се приема за отрицателно → σxmin (горните влакна са скъсени)
Б) в крайно долните - най-големите напрежения на опън σраст. Условно се приема за положителен → σxmax (долните влакна се удължават)
В) на нивото на неутралния слой (ос) σх = 0
7. Удълженията и съкращенията зависят от разстоянието до неутралния слой (ос)
8. Нормалните напрежения също зависят от това разстояние, т.е. те се променят линейно. Графика на промените в нормалните напрежения σx (диаграма на нормалните напрежения) - в
σхmax = σхmin = Mx : bh26 → σхmax= σхmin = MxWx
Момент на съпротивление WX = bh26 - геометричен индекс на съпротивление на правоъгълно сечениена огъване(таблична стойност)
(по аналогия ab е геометричен показател за съпротивлението на правоъгълно сечениена опън и натиск)
9. От формулата - ако размерите на гредата b и h са еднакви по дължината на гредата, тогава нормалните напрежения
σx пряко зависят от огъващия момент Mx - колкото по-голям е огъващият момент, толкова по-голямо е нормалното напрежение.
10. В средата на гредата огъващият момент достига максималната си стойност и → напреженията (max и min) ще бъдат най-големи за цялата греда.
1. Определя се по формулата на Журавски
Qx - напречна сила в разглежданото сечение
Sx - статичен момент на сечението (по формули или от таблици)
Jx - инерционен момент на сечението
b - ширина на сечението на лъча
Забележка. За описание на феномена на огъване се използват такива характеристики, които отчитат разпределението на материала по височината на сечението (тези характеристики се наричат геометрични)
2. От формулата - напреженията на срязване зависят от напречната сила Qx
А) където достигне максималната си стойност (тук: върху опорите), напреженията на срязване също ще бъдат най-големи.
B) където Qx = 0 (тук: в средата на лъча) → τу =0
3. Тангенциалните напрежения τу не се променят по линеен закон (като σx), а по закона на параболата
(τ зависи не само от Qx, но и от Sx - зависи от позицията на точката по височината на сечението)
4. Графиката на промените на напрежението по височината на сечението се нарича диаграма (r - парцел Q)
5. За по-голяма яснота промяната в срязващите и нормалните напрежения е показана в перспектива
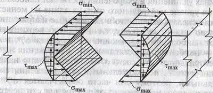
1. Нормалните напрежения са насочени хоризонтално (по оста x) → индекс x
2. Напреженията на срязване са насочени вертикално (по оста y) → индекс y
3. По отношение на инерционния момент J, момента на съпротивление W, статичния момент S - долният индекс (Jx Wx Sx или y) показва оста, спрямо която се изчисляват характеристиките.
Основни проектни допускания за огъване
1. Плосък участък, перпендикулярен на оста на недеформиран прът, остава плосък и нормален спрямо извитата ос на пръта след огъване (хипотеза за плосък участък)
2. Надлъжните влакна не се притискат един друг, когато се деформират
Анализ на якостта на греди
1.При нормални напрежения
σbendmin, min Rbend
Rizg - проектно съпротивление на материала при работа при огъване (таблична стойност)
σbend = МxWx → МхWx Rbend
2. Три вида проблеми при изчисляване на якостта на огъване (както при опън и компресия)
А) определяне на носещата способност на гредата
Б) проверка на носещата способност на гредата
C) избор на секцията на лъча (по-често)
2.Чрез напрежения на срязване
τmax R изместване
Rsdv - проектно съпротивление на материала при работа при срязване (таблични стойности. За стомана вместо Rsdv → Ravg)
QxSxJxb Rshift (изрязване)
Анализ на твърдостта на греди
1. Гредите могат да бъдат здрави и стабилни, но да имат прекомерни (повече от стандартните) отклонения
fmax fпред
fmax - максималното проектно отклонение на конструкцията
flimit - ограничаване на отклонението според SNiP
2. За междуетажни етажи flim = 1200 l, тавански подови греди flim = 1150 l
където l е дължината на обхвата на гредата
Интеграл на Мор и правило на Верещагин
1. Интегралът на Мор ви позволява да определитеогъвания и ъгли на въртенена дадена секциягреди с помощта на интегрално смятане.