Нелинейни алгоритми за управление
контролно устройство
значително разширява възможностите за целесъобразна промяна в качеството на процесите на управление. Това е ясно от общи фундаментални съображения, тъй като областта на нелинейните уравнения е много по-богата и по-разнообразна от линейните.
Въпреки факта, че няма обща теория на нелинейните алгоритми, изследванията и опитът в прилагането на някои конкретни типове от тези алгоритми показват тяхната голяма практическа ефективност. Това предполага уместността на тяхното теоретично изследване.
Нека въведем следната класификация на нелинейните алгоритми:
функционални нелинейни алгоритми;
логически нелинейни алгоритми;
оптимизиране на нелинейни алгоритми;
параметрични нелинейни алгоритми.
Важна разлика между нелинейните и линейните алгоритми е, че те придават принципно нови свойства на системата. Ако с линеен алгоритъм винаги се генерира сигнал, който е пропорционален на входната променлива или нейната производна и т.н., тогава с нелинеен алгоритъм самото естество на действието на системата за управление върху обекта може да се промени значително в зависимост от величината на входното действие. С други думи, ако за линейните системи промяната в размера на отклонението е само промяна в мащаба, а не във формата на процеси, тогава в нелинейна система формата на процесите също може да се промени значително, до фундаментални качествени промени в модела на процесите. Тези специални свойства на нелинейните алгоритми могат да бъдат изгодно използвани в инженерството за автоматично управление.
Нека разгледаме отделно всеки от тези четири класа нелинейни алгоритми.
Функционални нелинейни алгоритми за управление. Функционални алгоритми ще наричаме такива нелинейни алгоритми, при които управляващото въздействие върху обекта се изразява във форматанелинейна функция на отклонението на нейната стойност, която е входна информация за системата.
Този клас може да съдържа както статични, така и динамични нелинейности. Примери за статични характеристики:
За разлика от линейно пропорционалното, тук в първия случай ще има по-енергично действие на управляващото устройство за големи отклонения x и по-голям запас на устойчивост за стабилно състояние. Във втория случай ще има по-малко енергично, но по-плавно действие в началото и повишена точност в стационарно състояние, макар и с по-малка граница на стабилност. Подобни препоръки обаче, както ще видим по-късно, са валидни за повечето системи, но все пак не за всички. Затова те изискват специално проучване за всеки обект.
Нелинейният алгоритъм поради допълнителни нелинейни обратни връзки може също да включва нелинейности от изходната стойност и:
което разширява възможностите за целесъобразна промяна в качеството на управленския процес.
Примери за динамични характеристики в алгоритъма за управление:
където вместо двоен знак се има предвид един от тях.
Такива динамични условия влияят на свойствата на затихване на системата при преходни процеси по различен начин, в зависимост от размера и скоростта на отклонението. Те могат също така значително да подобрят динамичната точност (т.е. да намалят динамичните грешки) на системата в различни режими на принудително движение, възпроизвеждане на различни форми на дадени входни сигнали, а също и при произволни влияния.
системата може да превключва от едно устройство за линейна корекция към друго.
Логически нелинейни алгоритми за управление. Законите за нелинейно управление могат да имат други форми, които се прилагатизползвайки не функционални, а повече или по-малко сложни логически устройства. Ще ги наречем логически нелинейни алгоритми,
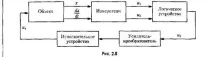
Например в системата на фиг. 2.8, може да се приложи логически нелинеен алгоритъм за запазване на контролни действия върху обект (както и спестяване на потребление на енергия за нуждите на контрола).
(ориз.
контролирана стойност (фиг. 2.8).
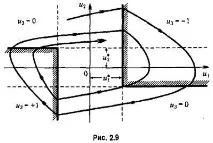
съвпада със знака на отклоненията, тогава големината на отклонението x модулно нараства. В този случай е необходимо енергично действие на управляващото устройство за отстраняването му.
, Тези съображения ни позволяват да считаме за целесъобразно, например, прилагането на следния логически закон за управление.
. Тази система ще бъде разгледана по-подробно в раздел IV.
. Ако правилно формирате логиката на тези превключватели, можете значително да подобрите качеството на системата.
Вместо да се комбинират тези линейни термини, могат да се въведат и функционални нелинейни термини; включването и изключването на сигналите, съответстващи на тези членове, се извършва от логическата единица. След това получавате комбинация от функционални и логически нелинейни алгоритми.
Оптимизиране на нелинейни алгоритми за управление. Автоматичната система се нарича оптимална, ако е най-добрата в определен смисъл, като се вземат предвид ограниченията, наложени върху големината на управляващото действие, координатите, скоростите и т.н. Това може да бъде например система, която има максимална скорост, или минимална консумация на енергия за управление, или максимална ефективност,
По правило това води до нелинейни алгоритми за управление, въпреки че най-общо казано е възможно да се оптимизират коефициентите на линеен алгоритъм чрез уточняване на неговата форма. Често оптималният нелинеен алгоритъм епревключване на управляващото действие (при определени състояния на системата) от една максимална възможна стойност към други. Времената на превключване обикновено се определят от сложни комбинации от стойностите на няколко променливи и техните производни.
, т.е. тези величини, в които се изразява параметричната програма.
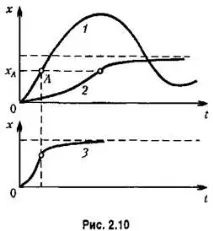
Алгоритмите за нелинейно управление имат богати възможности във всички случаи, когато желаният ефект може да бъде постигнат чрез промяна на свойствата на системата с промяна на стойностите на грешката.
Големи допълнителни възможности за подобряване на процесите на управление се осигуряват от нелинейно управление на работата на обекта чрез промяна на структурата на управляващото устройство в зависимост от размера и знаците на входните стойности, идващи от измервателното устройство.
(фиг. 2.11).
Ако в такава система всички връзки са линейни, тогава поради посоченото превключване, което се случва автоматично в процеса на управление, системата става нелинейна. Това може да се сравни с това как се получава нелинейна статична характеристика от прави сегменти. Но тук има нелинейна динамична характеристика, която е съставена от последователност от различни линейни диференциални уравнения, съответстващи на първия и втория алгоритми за управление.
По принцип работата на превключващо устройство в система с променлива структура може да възникне от няколко входни стойности. В този случай, в допълнение към основната нелинейност, възникваща поради превключването на структурата, може допълнително да има всякакви нелинейни свойства в отделни други връзки на управляващото устройство или обект.